sábado, 7 de enero de 2023
Creación de un entorno virtual Python y de un proyecto Django
sábado, 19 de noviembre de 2022
Redes neuronales desde cero
Una red neuronal artificial (o red neuronal para abreviar) es un modelo predictivo motivado por la forma en que funciona el cerebro. Pensemos en el cerebro como una colección de neuronas conectadas entre sí. Cada neurona mira las salidas de las otras neuronas que la alimentan, hace un cálculo, y luego se dispara (si el cálculo excede algún umbral) o no (si no lo hace).
En consecuencia, las redes neuronales artificiales constan de neuronas artificiales, que funcionan de esta manera. Las redes neuronales pueden resolver una amplia variedad de problemas como reconocimiento de escritura a mano y detección de rostros, y se utilizan mucho en el aprendizaje profundo, uno de los subcampos más de moda de la ciencia de datos. Sin embargo, la mayoría de las redes neuronales son "cajas negras"- inspeccionar sus detalles no nos dará mucha comprensión de cómo están resueltos los problemas. Y las grandes redes neuronales pueden ser difíciles de entrenar.
Perceptrones
El equivalente electrónico de una neurona es el perceptrón, con n entradas binarias. Calcula una suma ponderada de sus entradas y "dispara" si esa suma ponderada es cero o mayor:
def funcion_escalon(x):
return 1 if x >= 0 else 0
def psalida_perceptron(pesos, sesgo, x):
"""devuelve 1 si
el perceptrón se 'activa' y 0 si no lo hace"""
calcula = punto(pesos, x) + sesgo
return funcion_escalon(calcula)
El perceptrón simplemente distingue entre los medios espacios separados por el hiperplano de puntos x para el cual:
punto(pesos,x) + sesgo == 0
Con pesos elegidos correctamente, los perceptrones pueden resolver una serie de problemas simples ver figura.
Por ejemplo, podemos crear una puerta AND (que devuelve 1 si ambas entradas son 1 pero devuelve 0 si una de sus entradas es 0) con:
#Definición de puerta AND
pesos = [2, 2]
sesgo = -3
Si ambas entradas son 1, el cálculo es igual a 2 + 2 - 3 = 1 y la salida es 1. Si solo una de las entradas es 1, el cálculo es igual a 2 + 0 - 3 = -1, y la salida es 0. Y si ambas las entradas son 0, el cálculo es igual a -3 y la salida es 0. Del mismo modo, podríamos construir una puerta OR con:
#Definición puerta OR
pesos = [2, 2]
sesgo = -1
Y podríamos construir una puerta NOT (que tiene una entrada y convierte 1 a 0 y 0 a 1) con:
#Definición de puerta NOT
pesos = [-2]
bias = 1
Sin embargo, hay algunos problemas que simplemente no pueden resolverse con un solo perceptrón. Por ejemplo, no importa cuánto lo intentemos, no podemos utilizar un perceptrón para construir una puerta XOR que genera 1 si exactamente una de sus entradas es 1 y 0 en caso contrario. Aquí es donde empezamos necesitando redes neuronales más complejas.
Por supuesto, no es necesario utilizar una neurona (perceptrón) para construir una puerta lógica lo podemos hacer fácilmente por programación tradicional.
puerta_and = min
puerta_or = max
puerta_xor = lambda x, y: 0 if x == y else 1
Al igual que las neuronas reales, las neuronas artificiales comienzan a volverse más interesantes cuando comenzamos a conectar muchas.
Redes neuronales de realimentación positiva (avance)
La topología del cerebro es enormemente complicada, por lo que es común aproximarla con una red neuronal de realimentación idealizada que consta de capas discretas de neuronas, cada uno conectado al siguiente. Esto normalmente implica una capa de entrada (que recibe entradas y las alimenta sin cambios), una o más "capas ocultas" (cada una de las cuales consta de neuronas que toman las salidas de la capa anterior, realizan algunos cálculos y pasan el resultado a la siguiente capa) y una capa de salida (que produce las salidas finales).
Al igual que el perceptrón, cada neurona (no las de entrada) tiene un peso correspondiente a cada una de sus entradas y un sesgo. Para simplificar nuestra representación, agregaremos el sesgo al final de nuestro vector ponderado y daremos a cada neurona una entrada de sesgo que siempre es igual a 1.
Al igual que con el perceptrón, para cada neurona resumiremos los productos de sus entradas y sus pesos. Pero aquí, en lugar de generar una función escalón, generaremos una aproximación suave de la función de paso. En particular, utilizaremos el sigmoide :
#Función sigmoide
def sigmoide(t):
return 1 / (1 + math.exp(-t))
¿Por qué utilizar un sigmoide en lugar de una función de escalón más simple? Para entrenar una red neuronal, necesitaremos utilizar cálculo diferencial, y para esto, necesitamos funciones derivables. La función de paso ni siquiera es continua y por tanto no es derivable, la función sigmoide es una buena aproximación derivable de la misma.
La función sigmoide, también se llama función logística. Técnicamente "sigmoide" se refiere a la forma de la función, "logística" a esta función en particular.
Luego calculamos la salida como:
def salida_neurona(pesos, entradas):
return sigmoide(punto(pesos, entradas))
Dada esta función, podemos representar una neurona simplemente como una lista de pesos cuya longitud es uno más que el número de entradas a esa neurona (debido al peso del sesgo). Entonces nosotros podemos representar una red neuronal como una lista de capas (sin entrada), donde cada capa es el número de neuronas en esa capa. Es decir, representaremos una red neuronal como una lista (capas) de listas (neuronas) de listas (pesos).
Dada tal representación, utilizaremos una red neuronal es bastante simple:
def red_secuencial(red_neuronal, vector_entrada):
"""toma una red neuronal
(representada como una lista
de listas de listas de pesos)
y devuelve la salida desde la
entrada propagada hacia adelante"""
salidas = []
# procesa una capa cada vez
for capa in red_neuronal:
entrada_con_sesgo
=
vector_entrada + [1] # añade el sesgo de entrada
salida = [salida_neurona(neurona,
entrada_con_sesgo) # calcula la salida
for neurona in capa] # para cada neurona en la capa
salidas.append(salida) # la recuerda
# entonces, la entrada a la siguiente capa es la salida de
cada una
vector_entrada = salida
return salidas
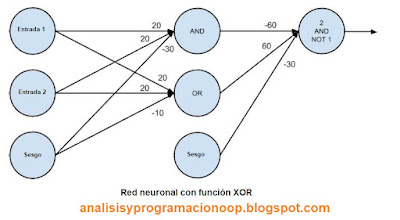
Ahora es fácil construir la puerta XOR que no podríamos construir con un solo perceptrón. Nosotros solo necesitamos escalar los pesos para que las salidas de cada neurona estén realmente cerca de 0 o muy cerca de 1:
red_xor = [# capa oculta
[[20, 20, -30], # neurona'and'
[20, 20, -10]], # neurona 'or'
# capa de salida
[[-60, 60, -30]]] # ' segunda entrada pero no primera entrada en una neurona
for x in [0, 1]:
for y in [0, 1]:
# red_secuencial produce las salidas de
cada neurona
# red_secuencial[-1] son las salidas de
las neuronas de las capas de salida
# print (x, y, red_secuencial(red_xor,[x,
y])[-1]) Esta línea no funciona, si alguien nos puede ayudar...
print (x, y)
# 0 0 [9.38314668300676e-14]
# 0 1 [0.9999999999999059]
# 1 0 [0.9999999999999059]
# 1 1 [9.383146683006828e-14]
El print nos da error, así que lo hemos dejado en un print más sencillo, si alguien sabe como evitar dicho error, que lo indique.
Al utilizar una segunda capa (capa oculta), podemos alimentar la entrada de una neurona "y" y la entrada de una neurona "o" con la salida de la neurona “y” lo que la convierte en en una neurona de "segunda capa o capa oculta”. El resultado es una red que realiza "o, pero no y", que es precisamente XOR
Por lo general, no construimos redes neuronales a mano. Esto se debe en parte a que las utilizamos para resolver problemas mucho mayores: un problema de reconocimiento de imágenes puede involucrar cientos o miles de neuronas. Y es en parte porque normalmente no podemos "razonar" lo que deberían hacer todas y cada una de estas neuronas. En vez de eso, “entrenamos” la red con datos. Un enfoque popular es un algoritmo llamado retropropagación que tiene similitudes con el algoritmo de descenso de gradiente.
Supongamos que tenemos un conjunto de entrenamiento que consta de vectores de entrada y el resultado correspondiente de vectores de salida. Por ejemplo, en nuestro ejemplo anterior, la red XOR, el vector de entrada [1, 0] correspondía a la salida de destino [1]. Imaginemos que nuestra red tiene un conjunto de pesos. Luego ajustamos los pesos usando el siguiente algoritmo:
Ejecutamos el algoritmo de realimentación positiva feed_forward en un vector de entrada para producir las salidas de todas las neuronas en la red.
Esto da como resultado un error para cada neurona de salida: la diferencia entre su salida y su objetivo.
Calculamos el gradiente de este error en función de los pesos de las neuronas y ajustamos sus pesos en la dirección que más disminuye el error.
"Propagamos" estos errores de salida hacia atrás para inferir errores para la capa oculta.
Calculamos los gradientes de estos errores y ajustamos los pesos de la capa oculta de la misma manera.
Por lo general, ejecutamos este algoritmo muchas veces para todo nuestro conjunto de entrenamiento hasta que la red converge:
def retropropagacion(red, vector_entrada, objetivos):
salidas_ocultas, salidas = red_secuencial(red, vector_entrada)
# la salida * (1 - salida) es de la derivada o sigmoide
salidas_incrementales = [salida * (1 - salida) * (salida - objetivo)
for salida, objetivo in zip(salidas, objetivos)]
# ajustamos los pesos para la capa de salida, una neurona cada vez
for i,
neurona_de_salida in enumerate(red[-1]):
# nos centramos en la i ésima salida de la capa neuronal
for j, salida_oculta in enumerate(salidas_ocultas + [1]):
# ajustamos el j ésimo peso basado en ambas:
# el incremental de la neurona y su j ésima entrada
neurona_de_salida[j] -= salidas_incrementale[i] * salida_oculta
# propagamos hacia atrás los errores de la capa oculta
incrementales_ocultas = [salida_oculta * (1 - salida_oculta) *
dot(salidas_incrementales
, [n[i] for n in capa_de_salida])
for i, salida_oculta in enumerate(salidas_ocultas)]
# ajustamos los pesos de la capa oculta, una neurona cada vez
for i, neurona_oculta in enumerate(red[0]):
for j, input in enumerate(vector_entrada + [1]):
neurona_oculta[j] -=
incrementales_ocultas[i] * input
Esto es prácticamente lo mismo que si escribiéramos explícitamente el error al cuadrado como una función de los pesos y usáremos la función minimo_estocastico.
En este caso, escribir explícitamente la función de gradiente resulta ser una molestia. Si conocemos el cálculo y la regla de la cadena, los detalles matemáticos son relativamente sencillos, pero manteniendo la notación correcta ("la derivada parcial de la función de error con respecto al peso que la neurona i asigna a la entrada procedente de la neurona j ”).
sábado, 13 de noviembre de 2021
Construyendo redes neuronales
Vamos a construir una red neuronal usando Python y Keras para clasificación con TensorFlow como backend. Keras es una biblioteca de Python poderosa y simplificada que podemos usar para construir redes neuronales y redes de aprendizaje profundo.
La primera tarea es importar todas las bibliotecas necesarias para TensorFlow y Keras. En la primera celda de código, especificamos las declaraciones para importar todas las bibliotecas necesarias para crear un entorno de TensorFlow.
from __future__ import absolute_import, division, print_function, unicode_literals
# TensorFlow y Keras
import tensorflow as tf
from tensorflow import keras
También necesitaremos algunas bibliotecas auxiliares. Importamos numpy y matplotlib. La tarea final consiste en imprimir la versión de TensorFlow para la que hemos especificado la versión de impresión en la última línea de la celda de código.
#librerías de ayuda
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
Al ejecutar esta celda, la última línea nos devuelve la versión de TensorFlow que tenemos instalada.
La siguiente tarea será cargar los datos para construir el modelo de red neuronal. Keras proporciona varios conjuntos de datos que podemos utilizar para construir un modelo de red neuronal. Utilizaremos un conjunto de datos llamado fashion_mnist, que contiene varias imágenes que se pueden clasificar en diferentes tipos.
dataset_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = dataset_mnist.load_data()
Para acceder al conjunto de datos fashion_mnist, declaramos una variable en la primera línea llamada dataset_mnist y le asignamos keras.datasets.fashion_mnist para cargar los datos en dicha variable. Los datos que estamos cargando ya están etiquetados, para el conjunto de entrenamiento, contamos con train_images y train_labels.
Y para el conjunto de prueba, se proporcionan test_images y test_labels. Para generar estos dos conjuntos diferentes de datos de prueba y de entrenamiento, llamamos a la función load_data.
La siguiente tarea consiste en definir varios tipos de clases. Hay varios tipos de clases que se pueden encontrar en el conjunto de datos fashion_mnist.
class_types
= ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
Hay diez etiquetas diferentes que se almacenarán en una matriz NumPy donde la primera etiqueta es asignada al número 0 y los números apuntarán a clases particulares. Por ejemplo, la etiqueta de la camiseta / top, 'T-shirt/top' será 0. La etiqueta para los pantalones 'Trouser' será 1 y así sucesivamente.
Al ejecutar la celda, se han definen los class_types. A continuación exploraremos los datos y el formato de los datos que usaremos para entrenar la red neuronal nuestro conjunto de entrenamiento.
train_images.shape
Si ejecutamos esta instrucción, nos muestra el número de imágenes y la forma de estas. Indica que hay 60.000 imágenes y el tamaño de cada imagen es de 28 por 28 píxeles.
len(train_labels)
Cuando ejecutamos la instrucción len(train_labels), la salida indica que hay 60.000 etiquetas en el conjunto de entrenamiento actual. Exploraremos las etiquetas en el conjunto de entrenamiento, que debería ser un número entero dentro de un rango particular.
train_labels
Al ejecutar esta línea, se muestra el siguiente resultado:
array([9, 0, 0, ..., 3, 0, 5], dtype = uint8
Esta matriz representa las etiquetas que están dentro del rango de 0 y 9.
Para ver el número de imágenes y su dimensión en el conjunto de datos de prueba, ejecutaremos.
test_images.shape
Después de la ejecución, se muestra el siguiente resultado: (10000, 28, 28). Que indica que hay 10.000 imágenes y el tamaño de cada imagen es de 28 por 28 píxeles.
Ahora vamos a preprocesar los datos de las imágenes. Para ello utilizaremos plt, que es un objeto de Matplotlib que importamos anteriormente.
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
Queremos inspeccionar la primera imagen y, para ello, hemos especificado las declaraciones plt.figure y plt.imshow. A la que le estamos pasando el índice 0 para obtener la primera imagen del conjunto de entrenamiento.
Tras la ejecución, se nos proporciona la primera imagen, pero no se escala correctamente. Así que la siguiente tarea consistirá en escalar la imagen.
train_images = train_images / 255
test_images
= test_images / 255
Hacemos lo mismo con test_images, para asegurarnos de que estamos escalando correctamente el valor de las imágenes de entrenamiento y las imágenes de prueba antes de que se envíen a la red neuronal. Las imágenes de entrenamiento de prueba se factorizarán en 255.
Ahora verificamos los datos, para ello, trazamos ciertos rangos de los datos, y usamos un tamaño de figura de 10 por 10. Y especificamos xticks e yticks, que representan el eje x y eje y.
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([ ])
plt.yticks([ ])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_types[train_labels[i]])
plt.show()
La declaración plt.imshow mostrará las imágenes. Después de extraerlas de train_images, la instrucción que tiene justo debajo garantiza que las imágenes estén etiquetadas con los tipos de clase adecuados.
Podemos observar que cada una de las imágenes están etiquetadas con sus respectivos tipos de clases. Habiendo explorado los datos, la siguiente tarea es construir el modelo de red neuronal. Para construir el modelo, primero configuraremos la etiqueta del modelo y luego compilaremos el modelo.
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation=tf.nn.relu),
keras.layers.Dense(10, activation=tf.nn.softmax)
])
Hemos especificado el modelo utilizando la declaración model = keras.Sequential. Y hemos agregado tres capas diferentes, la primera capa es la capa de entrada. La segunda capa es la capa oculta y la tercera capa es la capa de salida.
En la capa de entrada, estamos usando la función Aplanar (Flatten), a la que le estamos pasando el tamaño de entrada como 28 por 28, que es el tamaño real de la imagen. En la capa oculta, estamos usando la función Dense, a la que le estamos pasando un 128 como el número de nodos o neuronas, seguido de la función de activación relu. Finalmente, en la capa de salida estamos usando la función Dense y estamos pasando el valor del nodo como 10 seguido de la función de activación softmax.
La tarea final es compilar el modelo. Tenemos que compilar y configurar el modelo con ciertas configuraciones importantes antes de que el modelo esté listo para entrenarlo.
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
La primera parte contiene el optimizador, que indica cómo se actualiza el modelo en función de los datos proporcionados y la función de pérdida aplicada. La función de pérdida es la medida de precisión que generalmente está involucrada durante el proceso de entrenamiento.
La función de pérdida que hemos especificado es sparse_categorical_crossentropy. Las métricas, son el elemento de configuración final, se utilizan para especificar el aspecto de monitoreo de los pasos o procesos de capacitación y prueba. La métrica que hemos especificado es la precisión: accuracy.
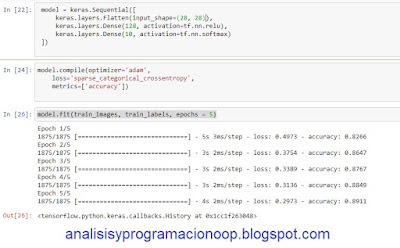
Hemos construido y compilado nuestro modelo con éxito, y podemos comenzar a usar la red neuronal para entrenar. Hay una última línea que entrena el modelo.
model.fit(train_images, train_labels,
epochs = 5)