El algoritmo de retropropagación trabaja llevando los datos de la capa de salida a la capa de entrada, propagando el error del gradiente a lo largo de la red. Una vez el algoritmo calcula el gradiente de la función de costo respecto a cada parámetro de la red, este utiliza estos gradientes para actualizar cada parámetro con el paso de descenso de gradiente.
Desafortunadamente, los gradientes a menudo se hacen cada vez más pequeños a medida que el algoritmo desciende hacia capas inferiores de la red, de modo que el Gradiente de Descenso deja las capas finales de la red prácticamente sin actualizar sus pesos impidiendo que la red alcance una buena solución. Esto se llama problema de los gradientes desaparecidos. En algunos casos puede suceder lo contrario, los gradientes pueden crecer hasta el punto de que en capas inferiores la actualización de pesos diverge explosivamente, este problema se conoce como de gradientes disparados, suele ser habitual en redes neuronales recurrentes.
Este problema mantuvo las redes neuronales sin avance durante los años 2000, pero comenzó a solucionarse con este paper de 2010.
En el que se comenzó a encontrar a los “sospechosos” entre ellos una combinación de la función de activación logística sigmoide y la técnica de asignación de pesos más popular por aquella época (distribución normal con una media de 0 y una desviación estándar de 1 cuando en realidad la función logística tiene una media de 0,5 y no de 0) Cuando las entradas toman valores grandes (positivos o negativos) la función de activación sigmoide se satura con valores de 0 o 1 con una derivada muy cercana a 0, de modo que la retropropagación empuja al gradiente a no propagarse a través de la red (o a dispararse).
La inicialización He
Para aliviar significativamente los problemas comentados, se propuso un flujo de la señal en ambas direcciones, hacia adelante cuando se han predicciones y hacia atrás con los gradientes de retropropagación, no se desea que la señal desaparezca o crezca exponencialmente, la solución que se propone es inicializar los pesos de cada capa de forma aleatoria. Para más información consultar el paper anteriormente reseñado.
Al final se han establecido diferentes algoritmos de inicialización en función de las funciones de activación que se vayan a utilizar estableciendo la siguiente tabla:
Inicialización Función de activación
Glorot Ninguna, tanh, logística, softmax
He ReLu, y sus variantes
LeCun SELU
Por defecto Keras utiliza la inicialización Glorot con una distribución uniforme. Cuando creamos una capa podemos cambiarla a inicialización He poniendo kernel_initializer=”he_uniform” o kernel_initializer=”he_normal” como esto.
A continuación unas líneas de código.
# Python ≥3.5
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# %tensorflow_version solo existe en Colab.
%tensorflow_version 2.x
except Exception:
pass
# TensorFlow ≥2.0
import tensorflow as tf
assert tf.__version__ >= "2.0"
# importaciones comunes
import numpy as np
import os
# para hacer este cuaderno estable
np.random.seed(42)
import tensorflow as tf
from
tensorflow import keras
#utilizamos la inicialización He normal
keras.layers.Dense(10,
activation="relu",
kernel_initializer="he_normal")
init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10,
activation="relu",
kernel_initializer=init)
Funciones de activación no saturantes
Se había asumido que si la madre naturaleza había establecido la función sigmoide como función de activación, esta sería una buena opción. Pero hay otras funciones de activación que funcionan mucho mejor en redes profundas, en particular la función de activación ReLU no se satura para valores positivos (y además es más rápida de computar).
Desafortunadamente ReLU no es perfecta y tiene sus propios problemas, durante el entrenamiento algunas neuronas “mueren” (sólo producen salida 0) en muchos casos puede morir hasta la mitad de las neuronas de nuestra red.
Una neurona “muere” cuando los pesos se han ajustado de tal forma que la suma de sus entradas es negativa para todas las instancias del conjunto de entrenamiento. Cuando sucede esto, todas sus salidas son cero y el Descenso de Gradiente no le afecta, porque el gradiente de ReLU es cero cuando la entrada es negativa. Para evitar este problema podemos utilizar Leaky ReLU.
En 2015 se propuso otra función de activación llamada ELU Exponential Linear Unit (ELU) que sobrepasa en ejecución a todas las variantes de ReLU anteriores pero también es más lenta.
En 2017 se introdujo la ELU escalada (Scaled ELU) o SELU
Como su nombre indica es una variante escalada de ELU. Si construimos una red neuronal compuesta exclusivamente de una pila de capas densas y todas las capas ocultas utilizando función de activación SELU, entonces la red tiende a auto-normalizarse, la capa de salida tiende a preservar de media el 0 y una desviación estándar de 1 durante el entrenamiento, lo cual resuelve el problema de los gradientes desaparecidos o disparados, de modo que la función de activación SELU tiene un comportamiento superior a cualquier otra, especialmente en redes profundas pero con condiciones:
-Las características de entrada deben ser estandarizadas (media 0, y desviación estándar de 1)
-Los pesos de cada capa deben estar inicializados con la inicialización normal LeCun en keras, del siguiente modo: kernel_initializer=”lecun_normal”
-La arquitectura de la red debe ser secuencial, si intentamos utilizar SELU en una red no secuencial, como por ejemplo una red recurrente o redes con saltos en las conexiones como Wide & Deep, la autonormalización no está garantizada.
- Todas las capas deben ser densas aunque también puede funcionar bien en redes convolucionales.
En general SELU > ELU> Leaky ReLU (y sus variantes)>ReLU>tanh>logística. Si la arquitectura de la red previene la autonormalización, ELU puede ser mejor que SELU y si la velocidad es nuestra prioridad, ReLU puede seguir siendo la mejor opción.
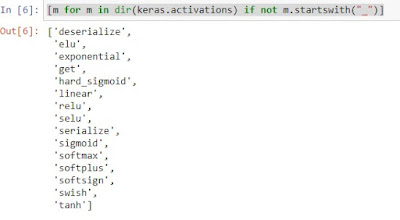
Aquí podemos ver las diferentes funciones de activación de Keras
[m for m in dir(keras.activations) if not m.startswith("_")]
Cargamos y tratamos nuestro dataset
#importamos nuestro dataset
import pandas as pd
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv') #tiene goles quiniela y quinigol
quinielas.head()
#las X contienen los datos relevantes para hacer predicciones quitamos
todas las etiquetas
#dejamos división, jornada, EquipoLocal, EquipoVisitante, PuntosLocal, PuntosVisitante,
Puntos_Normalizados
X = tf.cast(quinielas.drop(columns=['idPartido','temporada','golesLocal','golesVisitante','fecha','timestamp','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM']), tf.float64)
#las Y son las etiquetas a predecir, en este caso quitamos todo excepto
'Q1','QX','Q2'
y = tf.cast(quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp']), tf.float64)
x_data = np.array(X)
y_data = np.array(y)
#dividimos el dataset en una parte de entrenamiento y otra de testeo
train_data = x_data[:29718]
test_data = x_data[29718:]
train_labels = y_data [:29718]
test_labels =
y_data [29718:]
Ahora definimos el modelo con la activación He.
model = keras.models.Sequential()
model.add(keras.layers.Dense(300, kernel_initializer="he_normal"))
model.add(keras.layers.LeakyReLU())
model.add(keras.layers.Dense(100, kernel_initializer="he_normal"))
model.add(keras.layers.LeakyReLU())
model.add(keras.layers.Dense(3, activation="softmax"))
model.compile(loss="categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
#entrenamos y evaluamos el modelo
history = model.fit(train_data, train_labels, epochs=10,
validation_data=(test_data
, test_labels))
Notese que en la línea
model.add(keras.layers.Dense(3, activation="softmax
El 3 es el número de capas, si tenemos una red profunda de 10 o n capas ese número debe ser 10 o n.
Si queremos implementar la función ELU con Keras es trivial, basta con indicarlo al definir las capas
keras.layers.Dense(10,
activation="elu")
Para implementar SELU hacemos
keras.layers.Dense(10, activation="selu",
kernel_initializer="lecun_normal")
La definición completa del modelo SELU quedaría así.
#SELU
model = keras.models.Sequential()
model.add(keras.layers.Dense(300, activation="selu",
kernel_initializer="lecun_normal"))
for layer in range(99):
model.add(keras.layers.Dense(100, activation="selu",
kernel_initializer="lecun_normal"))
model.add(keras.layers.Dense(3,
activation="softmax"))
Normalización Batch
Aunque la inicialización He con la función de activación ELU o cualquier variante de ReLU puede reducir significativamente el peligro de los gradientes desaparecidos o disparados al comienzo del entrenamiento, no hay garantías de que no suceda durante el resto del entrenamiento. En un paper de 2015 se propuso una solución llamada Normalización por Lotes (Batch Normalization BN) Que trata de atajar este problema. La técnica consiste en añadir una operación al modelo justo antes o después de la función de activación de cada capa oculta. Esta operación simplemente centra en cero y normaliza cada entrada, entonces escala y mueve el resultado utilizando dos nuevos vectores de parámetros por capa: una para escalar y otro para mover.
Si utilizamos esta técnica al principio, en muchos casos no será necesario estandarizar nuestro set de entrenamiento, BN lo hará por nosotros. BN estandariza las entradas y reescala las salidas. BN mejora considerablemente la ejecución de todas la redes neuronales profundas, sobre todo es un gran avance para tareas de clasificación de imágenes (ImageNet).
Sin embargo BN añade complejidad al modelo (aunque nos elimina la necesidad de normalizar los datos antes) y también añade una penalización de tiempo, pues es algo más lenta.
Implementación de Normalización por Lotes
La implementación de BN en Keras es bastante sencilla e intuitiva
# Normalización por lotes
model = keras.models.Sequential([
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(3, activation="softmax")
])
Y esto es todo, en este caso hay solamente dos capas ocultas y la diferencia es pequeña, pero en una red profunda, la diferencia es considerable.
A veces, aplicar BN antes de la función de activación funciona mejor (hay un debate sobre este tema). Además, la capa antes de la capa BatchNormalization no necesita tener términos de sesgo, ya que la capa BatchNormalization los incluye, por lo que podemos establecer use_bias = False al crear esas capas:
model = keras.models.Sequential([
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(3, activation="softmax")
])
La clase BatchNormalization tiene unos pocos parámetros que podemos ajustar, si utilizamos los parámetros por defecto, normalmente funciona bien, pero ocasionalmente podemos necesitar ajustar el hiperparámetro momento (momentum), es utilizado para actualizar las medias de las capas de Normalización por Lotes. Un buen valor para el momento estará cercano a 1, 0,9, 0,99 Etc. son buenas opciones.
Otro hiperparámetro importante es el eje (axis) el cual determina el eje que debe ser normalizado. Por defecto es -1.