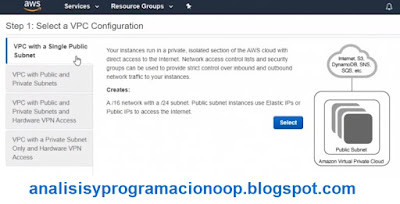
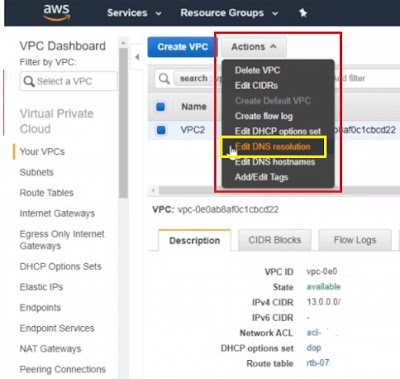
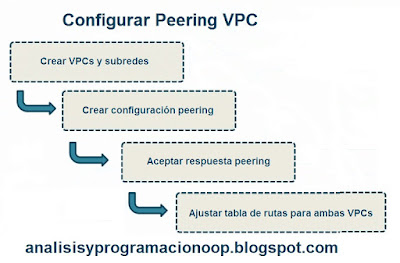
Los autoencoders
variacionales son bastante diferentes a los autoencoders vistos previamente, en
particular en estas dos características:
-
Son autoencoders probabilísticos, es decir
sus salidas son parcialmente determinadas aleatoriamente, incluso después de su
entrenamiento
-
Son autoencoders generativos. Es decir pueden
generar nuevas instancias similares a sus datos de entrenamiento.
Ejecutan una inferencia
Bayesana. Son similares al resto de los autoencoders, solo que para cada
entrada dada producen una codificación media y una desviación estándar. La
codificación real es entonces modificada aleatoriamente con una distribución
Gaussiana con la codificación media m y la desviación estándar s después
el decodificador decodifica la muestra normalmente .
El codificador genera m y
s y
lo codifica de forma aleatoria, luego lo decodifica y el resultado es una
instancia aleatoria pero similar a las de la entrada.
La estructura del
autoencoder se puede ver en la siguiente figura.
Aunque las entradas tengan
una distribución muy compleja, un autoencoder variacional tiende a producir
codificaciones (codings) similares a la distribución Gaussiana simple de las
muestras de entrada. Durante el entrenamiento la función de costo empuja a los
codings a migrar gradualmente dentro del espacio del coding (también llamado
espacio latente) hasta acabar pareciéndose a una nube de puntos Gaussianos. Una
gran consecuencia es que después de entrenar un autoencoder variacional podemos
fácilmente generar nuevas instancias simplemente eligiendo un punto aleatorio
dentro de nuestro espacio Gaussiano.
Es cuanto a la función de
costo, está compuesta por dos partes. La primera es la típica reconstrucción de
pérdida que empuja al autoencoder a reproducir sus entradas. Podemos utilizar
entropía cruzada para esta parte. La segunda parte es la perdida latente que
empuja al autoencoder a tener codings similares a las muestras de su
distribución Gaussiana: esto es la divergencia KL entre la distribución
objetivo (la distribución Gaussiana) y la distribución real del coding.
Vamos a comenzar
construyendo un autoencoder variacional para el dataset de moda MNIST. Lo
primero que necesitamos es una capa personalizada para los codings.
class Sampling(keras.layers.Layer):
def call(self, inputs):
mean, log_var = inputs
return K.random_normal(tf.shape(log_var)) * K.exp(log_var
/ 2) + mean
Esta capa de muestreo toma
dos entradas, la means (m) y la log_var(g). Utiliza la función K.random_normal()
para muestrear u vector aleatorio en el mismo espacio de g con
una media de 0 y una desviación estándar de 1donde luego lo multiplica por exp(g \2)
lo que lo convierte en s, y finalmente le añade m y
retorna el resultado.
Lo siguiente es crear el
codificador utilizando una API funcional ya que el modelo no es completamente
secuencial.
tf.random.set_seed(42)
np.random.seed(42)
codings_size = 10
inputs = keras.layers.Input(shape=[28, 28])
z = keras.layers.Flatten()(inputs)
z = keras.layers.Dense(150, activation="selu")(z)
z = keras.layers.Dense(100, activation="selu")(z)
codings_mean = keras.layers.Dense(codings_size)(z)
codings_log_var = keras.layers.Dense(codings_size)(z)
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = keras.models.Model(
inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])
Nótese que las capas densas que sacan codings_mean(m) y codings_log_var(g) tienen las
mismas entradas (las salidas de la segunda capa densa) entonces se pasan ambas
a la capa Sampling. Finalmente el modelo variational_encoder tiene tres salidas.
A continuación el decodificador.
decoder_inputs = keras.layers.Input(shape=[codings_size])
x = keras.layers.Dense(100, activation="selu")(decoder_inputs)
x = keras.layers.Dense(150, activation="selu")(x)
x = keras.layers.Dense(28 * 28, activation="sigmoid")(x)
outputs = keras.layers.Reshape([28, 28])(x)
variational_decoder = keras.models.Model(inputs=[decoder_inputs], outputs=[outputs])
Para este decodificador hemos utilizado la API
Secuencial en vez de la API Funcional, pues es más sencilla, una simple pila de
capas.
Finalmente construimos el modelo de autoencoder
variacional.
_, _, codings =
variational_encoder(inputs)
reconstructions =
variational_decoder(codings)
variational_ae = keras.models.Model(inputs=[inputs], outputs=[reconstructions])
Nótese que hemos ignorado las dos primeras salidas
del codificador (pues sólo queremos alimentar los codings del decodificador).
Finalmente debemos añadir la pérdida latente y la reconstrucción de pérdida.
latent_loss = -0.5 * K.sum(
1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss="binary_crossentropy", optimizer="rmsprop", metrics=[rounded_accuracy])
Primero calcula la pérdida
latent para cada instancia, luego calcula la pérdida media sobre todas las
instancias y divide el resultado entre 784 para asegurarse que tiene una escala
apropiada comparada con la recosntrucción de pérdida. Verdaderamente la
reconstrucción de pérdida del autodencoder variacional se supone como la suma
de los errores de reconstrucción de los pixels, pero cuando Keras calcula la
pérdida binary_crossentropy, lo
hace sobre la media de los 784 pixels más bien que con su suma.De modo que la reconstrucción de la pérdida es 784
veces más pequeña de lo que necesitamos. Para ello, definimos una pérdida
personalizada que calcula la suma en vez de la media. Para ello utilizamos el
optimizador RMSprop que funciona bien para este caso, y finalmente entrenamos
el modelo.
history = variational_ae.fit(X_train, X_train, epochs=25, batch_size=128,
validation_data=(X_valid,
X_valid))
Generando
imágenes de moda MNIST
Vamos a utilizar este
codificador variacional para generar imágenes similares a las que contiene el
dataset MNIST. Lo único que necesitamos son codings aleatorios procedentes de
una distribución Gaussiana y decodificarlos.
def plot_multiple_images(images, n_cols=None):
n_cols =
n_cols or len(images)
n_rows = (len(images) - 1) // n_cols + 1
if images.shape[-1] == 1:
images = np.squeeze(images, axis=-1)
plt.figure(figsize=(n_cols, n_rows))
for index, image in enumerate(images):
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(image, cmap="binary")
plt.axis("off")
Vamos a generar algunas
codificaciones aleatorias, decodificarlas y mostrar las imágenes resultantes:
tf.random.set_seed(42)
codings = tf.random.normal(shape=[12, codings_size])
images = variational_decoder(codings).numpy()
plot_multiple_images(images, 4)
save_fig("vae_generated_images_plot",
tight_layout=False)
La mayor parte de estas imágenes
parecen bastante convincentes, aunque son un poco borrosas. Vamos a ajustar un
poco mejor el autoencoder para hacerlas mejor.
Los autoencoders
variacionales, permiten ejecutar la interpolación semántica , en vez de
interpolar dos imágenes a nivel de pixel (lo qu emostrarís dos imágenes
solapadas) puede hacer la interpolación a nivel de coding. Tomamos dos imágenes
interpolamos sus codings y los decodificamos obteniendo una imagen final
similar a cualquier otra del dataset MNIST.
A continuación tomaremos 12
codings y los organizaremos en una matriz de 3X4, utilizando la función tf.image.resize() de
TensorFlow para redimensionar esta matriz a una de 5X7 . Por defecto la función
resize()
realiza interpolación linear de modo que cada imagen adicional contendrá
codings interpolados, finalmente decodificamos los codings para obtener las
imágenes.
tf.random.set_seed(42)
np.random.seed(42)
codings_grid = tf.reshape(codings, [1, 3, 4, codings_size])
larger_grid = tf.image.resize(codings_grid, size=[5, 7])
interpolated_codings = tf.reshape(larger_grid, [-1, codings_size])
images = variational_decoder(interpolated_codings).numpy()
plt.figure(figsize=(7, 5))
for index, image in enumerate(images):
plt.subplot(5, 7, index + 1)
if index%7%2==0 and index//7%2==0:
plt.gca().get_xaxis().set_visible(False)
plt.gca().get_yaxis().set_visible(False)
else:
plt.axis("off")
plt.imshow(image, cmap="binary")
save_fig("semantic_interpolation_plot",
tight_layout=False)
La imagen inferior muestra las imágenes resultantes. Las originales están
enmarcadas y el resto son el resultado de la interpolación semántica entre sus
imágenes cercanas. Nótese por ejemplo como el zapato de la cuarta fila es una
interpolación entre los que tiene encima y debajo.
Traducido del capítulo 17 de “Hands-On Machine Learning with Scikit-Learn, Keras and Tensorflow, 2nd Edition by Aurelien Géron (O’Reilly). Copyright 2019 Kiwisoft S.A.S., 978-1-492-03264-9”