Con frecuencia, en machinelearning, intentaremos encontrar el mejor modelo para una determinada situación. Y, por lo general, "mejor" significa minimizar el error del modelo o maximizar la probabilidad de los datos. En otras palabras, representará la solución a algún tipo de problema de optimización.
Esto significa que tendremos que resolver una serie de problemas de optimización. Y en particular, tendremos que resolverlos desde cero. El enfoque habitual es una técnica llamada descenso de gradiente, que se presta bastante bien a un tratamiento desde cero. Supongamos que tenemos alguna función f que toma como entrada un vector de números reales y como salida
un solo número real. Una simple función de este tipo sería así:
def suma_de_cuadrados(v):
"""calcula la suma de cuadrados en v"""
return sum(v_i ** 2 for v_i in v)
Con frecuencia, necesitaremos maximizar (o minimizar) dichas funciones. Es decir, tenemos que encontrar la entrada v que produce el valor más grande (o más pequeño) posible.
Para funciones como esta, el gradiente (el vector de derivadas parciales) da la dirección de entrada en la que la función aumenta más rápidamente. Por tanto para maximizar una función, elegimos un punto de partida aleatorio, calculamos el gradiente, y damos un pequeño paso en la dirección del gradiente (es decir, la dirección que hace que la función aumente más), y repetimos con el nuevo punto de partida. Del mismo modo, podemos intentar minimizar una función dando pequeños pasos en el sentido contrario.
Es importante tener en cuenta que si una función tiene un mínimo global único, es probable que este procedimiento lo encuentre. Pero si una función tiene múltiples mínimos (locales), este procedimiento puede "encontrar" el incorrecto, en cuyo caso podemos volver a ejecutar el procedimiento desde diversos puntos de partida. Si una función no tiene mínimo, entonces es posible que este procedimiento continúe para siempre.
Estimando el gradiente
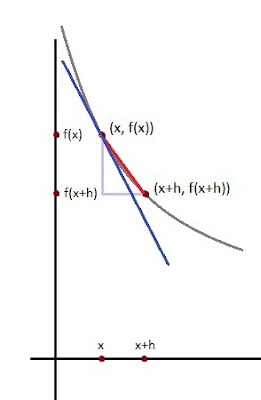
Si f es una función de una variable, su derivada en un punto x mide cómo cambia f (x), cuando hacemos un cambio muy pequeño a x. Se define como el límite de la diferencia de cocientes cuando h se acerca a cero.
def diferencia_de_cocientes(f, x, h):
return (f(x + h) - f(x)) / h
La derivada es la pendiente de la recta tangente a la función (azul) , mientras que el cociente de diferencias es la pendiente de la recta no tangente que la atraviesa (rojo).
Si h se hace cada vez más pequeña, la línea no tangente (roja) se acerca cada vez más a la tangente (azul).
Para muchas funciones, es fácil calcular exactamente las derivadas. Por ejemplo, para la función cuadrado:
def cuadrado(x):
return x * x
Tiene derivada
def derivada(x):
return 2 * x
Aunque no podemos calcular límites en Python, podemos estimar derivadas evaluando el cociente de la diferencia para un pequeño e.
from functools import partial
derivative_estimate = partial(diferencia_de_cocientes, cuadrado, h=0.00001)
x = range(-10,10)
Cuando f es una función de muchas variables, tiene múltiples derivadas parciales, cada una indicando cómo cambia f cuando hacemos pequeños cambios en solo una de las variables de entrada. Calculamos su i-ésima derivada parcial tratándola como una función solo de su i-ésima variable,
manteniendo las otras variables fijas:
def cociente_derivada_parcial(f, v, i, h):
"""calcula el cociente de la i-ésima diferencia de f a
v"""
w = [v_j + (h if j == i else 0) # suma h al i-ésimo elemento de v
for j, v_j in enumerate(v)]
return (f(w) - f(v)) / h
después de lo cual podemos estimar el gradiente de la misma manera:
def gradiente_estimado(f, v, h=0.00001):
return [cociente_derivada_parcial(f, v, i, h)
for i, _ in enumerate(v)]
Un inconveniente de este enfoque de "estimación utilizando cocientes de diferencias" es que es computacionalmente costoso. Si v tiene una longitud n, el gradiente_estimado debe evaluar f en 2n entradas diferentes. Si estimamos gradientes repetidamente, estamos obligando al procesador ha de realizar un montón de trabajo adicional.
Usando el gradiente
Es fácil ver que la función suma_de_cuadrados es más pequeña cuando su entrada v es un vector de ceros. Pero imaginemos que no lo sabemos. Utilizaremos gradientes para encontrar el mínimo entre todos los vectores tridimensionales. Simplemente elegiremos un punto de partida aleatorio y luego tomaremos pequeños pasos en la dirección opuesta del gradiente hasta llegar a un punto donde el gradiente es muy pequeño:
#definimos las funciones auxiliares previas
import math
def magnitud(v):
return math.sqrt(suma_de_cuadrados(v)) # math.sqrt es la función
raiz cuadrada
def resta_de_vectores(v, w):
"""resta los
elementos correspondientes"""
return [v_i - w_i
for v_i, w_i in zip(v, w)]
def distancia(v, w):
return magnitud(resta_de_vectores(v, w))
import random
def paso(v, direccion, tamaño_paso):
"""mueve el tamaño del paso en la dirección a
v"""
return [v_i + tamaño_paso * direccion_i
for v_i, direccion_i in zip(v, direccion)]
def suma_de_gradientes_cuadrados(v):
return [2 * v_i for v_i in v]
# toma un punto aleatorio para comenzar
v = [random.randint(-10,10) for i in range(3)]
tolerancia = 0.0000001
while True:
gradiente =
suma_de_gradientes_cuadrados(v) # calcula el gradiente de v
siguiente_v = paso(v, gradiente, -0.01) # toma un paso negativo de gradiente
if distancia(next_v, v) < tolerancia: # para si convergen
break
v = siguiente_v # continua en caso contrario
Si ejecutamos esto, encontraremos que siempre terminamos con una v muy cercana a [0,0,0]. Cuanto menor sea la tolerancia, más se acercará.
Elegir el tamaño de paso correcto
Aunque la razón fundamental para moverse en contra del gradiente es clara, la distancia a la que se debemos movernos no lo es. De hecho, elegir el tamaño de paso correcto es más un arte que una ciencia. Opciones populares consisten en:
Utilizar un tamaño de paso fijo
Reducir gradualmente el tamaño del paso con el tiempo
En cada paso, elegir el tamaño del paso que minimiza el valor de la función objetivo
El último suena óptimo pero, en la práctica, tiene un cálculo costoso. Podemos aproximarlo probando una variedad de tamaños de paso y elegir el que resulte en el valor más pequeño de la función objetiva:
Tamaño_paso = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001] Es posible que ciertos tamaños de paso den como resultado entradas no válidas para nuestra función. Así, pues tenemos la necesidad de crear una función de "aplicación segura" que devuelva infinito (que nunca debería ser el mínimo de cualquier cosa) para entradas no válidas:
def segura(f):
"""devuelve una funcion igual a f,
excepto que sus salidas no
devuelven error si tienden a infinito"""
def f_segura(*args, **kwargs):
try:
return f(*args, **kwargs)
except:
return float('inf') # 'inf' sugnifica
infinito en Python
return safe_f
Poniéndolo todo junto
En el caso general, tenemos una función objetivo objetivo_fn que queremos minimizar, y también tenemos su gradiente_fn. Por ejemplo, objetivo_fn podría representar los errores en un modelo como una función de sus parámetros, y es posible que deseemos encontrar los parámetros que cometan los errores tan pequeño como sea posible.
Además, digamos que hemos elegido (de alguna manera) un valor inicial para los parámetros theta_0. Entonces podemos implementar el descenso de gradiente como:
def minimiza_lote(objetivo_fn, gradiente_fn, theta_0, tolerancia=0.000001):
"""utiliza descenso de gradiente para encontrar el theta
que minimiza la función objetivo"""
tamaño_paso = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
theta = theta_0 # establece theta a su valor inicial
target_fn = segura(objetivo_fn) # devuelve la versión segura de la función objetivo_fn
valor = objetivo_fn(theta) # valor que estamos minimizando
while True:
gradiente = gradiente_fn(theta)
siguientes_thetas = [paso(theta, gradiente, -tamaño_paso)
for tamaño_paso in tamaño_pasos]
# elije el valor que minimiza la funcion de error
siguiente_theta = min(siguientes_thetas, key=objetivo_fn)
siguiente_valor = objetivo_fn(siguiente_theta)
# se detiene si está convergiendo
if abs(valor - siguiente_valor) < tolerancia:
return theta
else:
theta, valor =
siguiente_theta, siguiente_valor
Lo llamamos minimizar_lote porque, para cada paso de gradiente, analiza el conjunto de datos completo (porque objetivo_fn devuelve el error en todo el conjunto de datos). En la siguiente sección, veremos un enfoque alternativo que solo analiza un punto de datos a la vez.
A veces, en cambio, queremos maximizar una función, lo que podemos hacer minimizando su negativo (que tiene un gradiente negativo correspondiente):
def niega(f):
"""devuelve una función que por cada entrada x devuelve
-f(x)"""
return lambda *args, **kwargs: -f(*args, **kwargs)
def niega_todo(f):
"""lo mismo cuando f devuelve una lista de números"""
return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]
def maximiza_lote(objetivo_fn, gradiente_fn, theta_0, tolerancia=0.000001):
return minimiza_lote(niega(objetivo_fn),
niega_todo(gradiente_fn),
theta_0,
tolerancia)
Descenso de gradiente estocástico
Como mencionamos antes, a menudo usaremos el descenso de gradiente para elegir los parámetros de un modelo de una manera que minimice alguna noción de error. Usando el enfoque por lotes anterior, cada paso del gradiente requiere que hagamos una predicción y calculemos el gradiente para el conjunto de datos, lo que hace que cada paso lleve mucho tiempo. Por lo general, estas funciones de error son aditivas, lo que significa que el error predictivo en todo el conjunto de datos es simplemente la suma de los errores predictivos para cada punto de datos. Cuando este es el caso, podemos aplicar una técnica llamada descenso de gradiente estocástico, que calcula el gradiente (y da un paso) solo para un punto a la vez. Se repiten los datos hasta llegar a un punto de parada. Durante cada ciclo, queremos iterar a través de nuestros datos en un orden aleatorio:
def en_orden_aleatorio(dato):
"""generador que devuelve los elementos de los datos en
un orden aleatorio"""
indices = [i for i, _ in enumerate(dato)] # crea una lista de indices
random.shuffle(indices) # los baraja
for i in indices: # devuelve los datos en este orden
yield dato[i]
Y queremos dar un paso de gradiente para cada punto de datos. Este enfoque deja el posibilidad de que podamos dar vueltas cerca de un mínimo para siempre, por lo que cada vez que nos detenemos obteniendo mejoras, disminuiremos el tamaño del paso y, finalmente, abandonaremos:
def minimiza_estocastico(objetivo_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
dato = zip(x, y)
theta = theta_0 # valor inicial
alpha = alpha_0 # tañaño de paso inicial
min_theta, min_valor = None, float("inf") # el valor mínimo más lejano
iteracciones_sin_mejora = 0
# si tenemos 100 iteracciones sin mejora paramos
while
iteracciones_sin_mejora < 100:
valor = sum( objetivo_fn(x_i, y_i, theta) for x_i, y_i in dato )
if valor < min_valor:
# si encontramos un mínimo lo recordamos
# y regresamos al tamaño de paso original
min_theta, min_valor = theta, valor
iteracciones_sin_mejora = 0
alpha = alpha_0
else:
# en otro caso no tenemos mejora, así que intentamos
disminuir el tamaño del paso
iteracciones_sin_mejora += 1
alpha *= 0.9
# y tomamos un paso de gradiente para cada uno de los
puntos de datos
for x_i, y_i in
en_orden_aleatorio(dato):
gradiente_i = gradiente_fn(x_i, y_i, theta)
theta =
resta_de_vectores(theta, multiplicacion_escalar(alpha, gradiente_i))
return min_theta
La versión estocástica suele ser mucho más rápida que la versión por lotes. Por supuesto, queremos hacerlo con una versión que maximice también:
def maximiza_estocastico(objetivo_fn, gradiente_fn, x, y, theta_0, alpha_0=0.01):
return minimiza_estocastico(niega(objetivo_fn),
niega_todo(gradiente_fn),
x, y, theta_0, alpha_0)