Si estamos abordando un problema complejo sobre una tarea supervisada pero no disponemos de etiquetas para entrenar con los datos, una solución es encontrar una red neuronal que ejecute tareas similares y reutilizar sus capas inferiores. Esto hace posible entrenar modelos complejos utilizando pocos datos de entrenamiento aunque nuestra red neuronal no haya aprendido todas las características de bajo nivel; para ello utilizaremos los detectores de características aprendidos por una red existente.
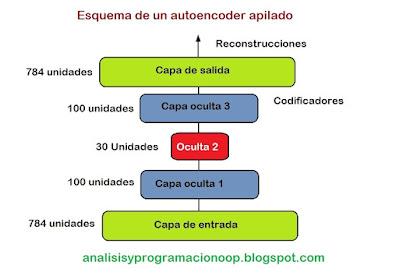
De modo análogo, si tenemos en dataset muy grande pero la mayoría no está etiquetado, podemos entrenar un autoencoder apilado utilizando todos los datos y luego reutilizar las capas más bajas entrenadas para crear una red neuronal para nuestra tarea definitiva utilizando estos datos etiquetados. Esto se muestra en la figura inferior, donde pre-entrenamos un autoencoder apilado con datos no etiquetados y luego congelamos las capas inferiores que ya están pre-entrenadas y las utilizamos como capas inferiores de la nueva red neuronal.
Es común tener muchos datos de los cuales sólo unos pocos etiquetados, construir un gran dataset no etiquetado es tan sencillo como descargar millones de imágenes de internet, pero etiquetar dichas imágenes correctamente, es una tarea que sólo los humanos podemos hacer de forma fiable. Etiquetar imágenes consume mucho tiempo y es costoso, con lo que es habitual tener sólo unos pocos miles de imágenes etiquetadas por humanos.
Utilizamos todo el dataset, tanto las imágenes etiquetadas como las que no lo están para entrenar nuestro autoencoder y reutilizamos las capas inferiores del autoencoder en nuestra nueva red neuronal.
Vamos a ver algunas técnicas para entrenar de este modo autoencoders.
Atando los pesos
Cuando un autoencoder es
exactamente simétrico una técnica común consiste en atar los pesos de las capas
del decodificador a los pesos de las capas del codificador. Esto reduce a la
mitad el número de pesos en el modelo, acelerando el entrenamiento y limitando
el riesgo de sobreentrenamiento. Si el autoencoder tiene N capas (sin contar la
capa de entrada), y WL
representa la conexión de los pesos a la capa L-ésima. Es decir la capa 1 es la
primera capa oculta N/2 es la capa de codificación (coding) y la capa N es la capa de salida,
entonces las capas del decodificador definen sus pesos como WN-L+1 = WLT (con L= 1,2,…..,N/2)
Los pesos atados entre capas utilizando keras son definidos por la capa personalizada.
Es común vincular los pesos del codificador y el decodificador, simplemente usando la transposición de los pesos del codificador como pesos del decodificador. Para esto, necesitamos usar una capa personalizada.
class DenseTranspose(keras.layers.Layer):
def __init__(self, dense, activation=None, **kwargs):
self.dense = dense
self.activation = keras.activations.get(activation)
super().__init__(**kwargs)
def build(self,
batch_input_shape):
self.biases = self.add_weight(name="bias",
shape=[self.dense.input_shape[-1]],
initializer="zeros")
super().build(batch_input_shape)
def call(self, inputs):
z = tf.matmul(inputs, self.dense.weights[0], transpose_b=True)
return self.activation(z + self.biases)
Esta capa personalizada actúa como una capa regular densa, pero utiliza los pesos de otra capa regular densa, trasponiendo ( poner transpose_b = True es equivalente a transponer el segundo argumento, pero es más eficiente que esto ejecutar la trasposición sobre la marcha dentro de la operación matmul) Sin embargo esto utiliza su propio vector de sesgo (bias). Lo siguiente es construir un nuevo autoencoder apilado, similar al anterior pero con las capas densas del decodificador atadas a las capas densas del codificador.
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
dense_1 = keras.layers.Dense(100, activation="selu")
dense_2 = keras.layers.Dense(30, activation="selu")
tied_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
dense_1,
dense_2
])
tied_decoder = keras.models.Sequential([
DenseTranspose(dense_2, activation="selu"),
DenseTranspose(dense_1, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
tied_ae = keras.models.Sequential([tied_encoder, tied_decoder])
tied_ae.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1.5), metrics=[rounded_accuracy])
history = tied_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid,
X_valid))
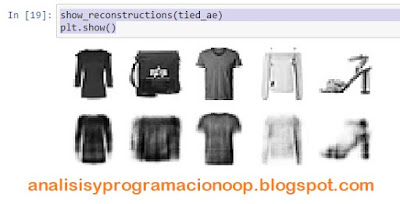
Este modelo tiene una ejecución de reconstrucción ligeramente inferior al anterior pero con la mitad de parámetros.
show_reconstructions(tied_ae)
plt.show()
Traducido del capítulo 17 de “Hands-On Machine Learning with Scikit-Learn, Keras and Tensorflow, 2nd Edition by Aurelien Géron (O’Reilly). Copyright 2019 Kiwisoft S.A.S., 978-1-492-03264-9”