SQL Server y Programación Orientada a Objetos, .NET, Visual Basic, Bases de Datos, Electrónica y mucho más...
Regresión Logística para clasificadores de Machine Learning I: la curva de regresión logística.
Regresión logística y clasificación para Machine Learning II. Clasificación
Regresión logística y clasificación para Machine Learning III. Keras
Regresión logística y clasificación para Machine Learning IV. Preparación de datos
Regresión logística y clasificación para Machine Learning V. Red Neuronal keras-tensorflow
En este post trataré de ofrecer una comprensión conceptual de cómo funcionará un modelo de regresión logística con Keras, pues Keras es muy utilizado para construir redes neuronales.
Antes de nada, veremos cómo se puede utilizar sólo una neurona para realizar una regresión lineal. Una vez que introducimos los datos de entrenamiento, la neurona realizará una transformación en la forma Y = Wx + b, que es la ecuación de una línea recta. El propósito de este entrenamiento es encontrar los valores óptimos de W (los pesos de la entrada) y b (el desplazamiento respecto al eje o sesgo [bias]), para minimizar la pérdida de datos de entrenamiento. Hecho esto, tenemos un modelo de regresión lineal con los valores óptimos de W y b. Esta es la red neuronal más simple posible, donde solo tenemos una neurona y esta realiza una transformación lineal simple. Si hacemos zoom en la neurona, vemos que hay una serie de entradas diferentes W. Dentro de la neurona hay dos funciones. Una de ellas es una transformación lineal y las entradas de esta, que serán las entradas de la propia neurona. La otra es la función de salida de dicha transformación lineal que alimenta una función de activación. El propósito de la función de activación es introducir un elemento de no linealidad en la salida de la neurona.
Esta no linealidad es necesaria para capturar relaciones más complejas entre la entrada y la salida, lo que se aplica a la mayoría de los casos de uso de redes neuronales. Sin embargo, si estamos utilizando una red neuronal de este tipo para hacer una regresión lineal, no necesitamos este componente no lineal en la neurona. Y podemos transmitir la transformación lineal con una función de identidad. Esto garantiza que la salida de la neurona sea, de hecho, la salida de la propia transformación lineal.
Para realizar una regresión logística, podemos reemplazar esta función de identidad por una función softmax. La función softmax asegura que la salida de nuestra neurona sea categórica. Es decir, si queremos que esta neurona realice una clasificación binaria, podemos configurar la función softmax para producir dos o n salidas. De esta forma, una vez que introducimos todas las entradas en esta neurona, la combinación de la transformación lineal y la función softmax producirá dos posibilidades de salida (activada y no activada o 1 y 0), que corresponde a las dos categorías distintas. También hay que tener en cuenta que nuestra transformación lineal incluirá un valor de sesgo además de los pesos de la entrada. La combinación de esta transformación lineal y la función softmax terminará produciendo una regresión logística. El resultado de esta regresión logística podría ser una probabilidad de que un evento en particular sea falso. Y la probabilidad de que el mismo evento sea cierto es simplemente 1 menos la probabilidad de que sea falso.
Si echamos un vistazo más cercano al componente softmax. Podemos decir que cualquier entrada x que entre en una función softmax, que esté configurada para generar valores verdaderos o falsos (true o false), producirá dos salidas distintas. Una que contiene la probabilidad de que el evento sea falso y la otra de que el evento sea verdadero.
La función softmax (también llamada exponencial normalizada) se puede ampliar para realizar la clasificación de N categorías. Cuando definimos una función softmax para nuestro modelo, podemos configurarla para generar N categorías diferentes en lugar de dos. La función softmax generará puntuaciones de probabilidad para cada categoría de salida. Y la categoría que tenga la mayor probabilidad se elegirá como predicción del modelo. Una vez hayamos configurado nuestra red neuronal poniendo en la última capa una salida softmax. La salida de nuestro modelo corresponderá al número de categorías diferentes que pueda tomar la salida. Y cada una de estas categorías estará asociada con una puntuación de probabilidad.
Esto se llama Regresión Logística Multinomial o Regresión Softmax. El clasificador por Regresión Softmax predice sólo una clase cada vez. Es decir, es multi-clase, no multi-salida. Por lo que debe ser utilizado solamente para clases mutuamente excluyentes, como el caso que hemos visto de las diferentes flores, pero no deberá ser utilizado por ejemplo, para reconocer a múltiples personas en un cuadro.
Una vez Softmax ha calculado la probabilidad de una instancia de pertenecer a cada clase, comparamos los resultados de salida con los datos reales, para ver lo acertados o fallidos que han sido. Y realimentar nuestro modelo para que mejore sus predicciones. Esta comparación se realiza con una función llamada Entropía Cruzada y trata de minimizar la llamada función de costo de la salida, que es el error cometido en cada predicción.
La Entropía Cruzada se originó a partir de la teoría de la información. Supongamos que queremos transmitir eficientemente todos los días la información del tiempo desde una estación hasta una emisora. Si tenemos ocho posibles tipos de tiempo. Soleado, nublado, nubes y claros, lluvioso, ventoso, etc necesitamos utilizar tres bites de información 2 elevado a 3= 8. Si embargo si la mayor parte del tiempo es soleado podemos ser más eficientes codificando soleado sólo con un bit (0) y las otras siete opciones con cuatro bits comenzando por 1 seguido de los tres bits restantes. La entropía cruzada mide el número medio de bits que enviamos realmente en cada opción. Si la estación meteorológica se encuentra en un desierto y asumimos que el tiempo es casi siempre soleado, la entropía cruzada será igual que la entropía del propio tiempo (intrínsecamente impredecible). Pero si hacemos una mala asunción (es decir en realidad, llueve con frecuencia) la entropía cruzada será grande.
Por otro lado, si las distribuciones de probabilidad reales están muy desincronizadas con las predicciones, lo que tenemos es un valor muy alto de entropía cruzada. En el caso de una regresión lineal, el objetivo sería minimizar el error cuadrático medio, que es una función de pérdida comúnmente utilizada. Pero en el caso de un modelo de clasificación, el objetivo es minimizar la entropía cruzada. Las funciones de entropía cruzada en la mayoría de las bibliotecas de aprendizaje automático realizarán algún tipo de estimación de las distribuciones de probabilidad de los valores reales.
Hasta ahora, los problemas de clasificación que hemos discutido simplemente han involucrado clasificación binaria, que es la forma más simple. Sin embargo, si nuestra salida debe tener N categorías diferentes, necesitamos alguna forma de manejar esto en un clasificador. Esto será especialmente útil para identificar letras o números manuscritos, o si nuestro modelo está destinado a clasificar imágenes.
En este post veremos cómo utilizar el concepto de regresión logística para resolver problemas de clasificación. En cualquier clasificación, primero observaremos los atributos de los datos que tenemos. Y luego, basándonos en esos atributos, realizaremos una categorización o clasificación. La forma más simple de clasificación es una clasificación binaria, en la que solo tenemos dos resultados posibles. Por ejemplo, si un correo electrónico ingresa en nuestra bandeja de entrada, tendremos que clasificarlo como spam o genuino es decir, como correo electrónico auténtico.
En un problema de regresión logística, lo que estamos tratando de predecir es una probabilidad que toma valores entre cero y uno. (en realidad entre 0 y 100%) esto se puede trazar mediante una curva en S.
Una vez completada la capacitación, lo que queda es un modelo de regresión logística, que puede utilizarse para hacer predicciones. Una vez que tengamos nuestro clasificador basado en aprendizaje automático, podemos asegurarnos de que cuando un correo electrónico llegue a nuestra bandeja de entrada, este se envíe a este clasificador. Basado en lo que ha aprendido durante la capacitación, el modelo tomará una decisión. Si el correo electrónico es genuino o es spam.
Esta es la región de regresión logística del modelo, que es muy sensible a cualquier cambio en la entrada. Puede haber algunas características en el correo electrónico que hagan que nuestro modelo de regresión logística decida que hay un 99% de probabilidad de que se trate de spam. Nuestro modelo puede calcular un solo valor de probabilidad. Si necesitamos realizar una clasificación utilizando este modelo de regresión logística, deberemos establecer un umbral. La regla del 50% dicta que, en caso de una clasificación binaria, este umbral debe establecerse en una probabilidad del 50%.
Por lo tanto, cualquier probabilidad de spam inferior al 50% debe clasificarse como genuino, y cualquier probabilidad mayor debe marcarse como spam. Si solo hay dos resultados posibles para este clasificador, cada uno de ellos opera sobre un rango de valores de probabilidad. La combinación de la curva S de regresión logística y el establecimiento de un valor umbral, nos ayudará a realizar la clasificación.
Los algoritmos de regresión logística pueden ser utilizados para clasificación (fundamentalmente binaria ver esquema general de IA). Son utilizados para estimar la probabilidad de que una instancia pertenezca a una clase particular o no. De modo que si la probabilidad de pertenecer a una clase A es superior a 50% el modelo predice que esa instancia pertenece a la clase A y la etiqueta como 1. En caso contrario, predice que no pertenece y la etiqueta como 0. Esto forma un clasificador binario.
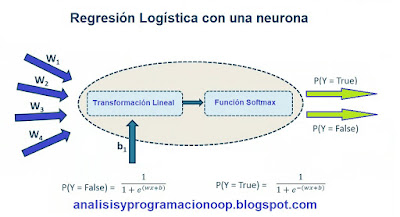
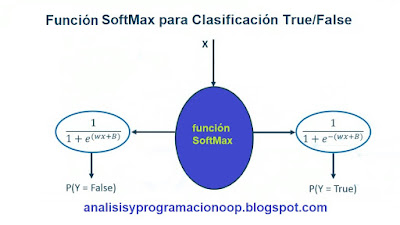
Un modelo de regresión logística computa una suma ponderada de características de entrada (más un término de desplazamiento) y da como resultado un porcentaje entre 0 (0) y 100% (1). Su función es una sigmoide.
En el modelo concreto de arriba el 50% está justo para t=0 de modo que podemos decir que la predicción de este modelo es de 0 para t<0 y 1 para t >0.
Este tipo de función es especialmente adecuado para características separadas que se unen en un estrecho rango. Por ejemplo a la hora de distinguir entre dos especies de flor Iris Virgínica o Iris Versiocolor en función de la longitud de sus pétalos. O bien las posibilidades de default de un pagador frente a su acreedor en función del tiempo que tarda en devolver el préstamo.
Así por ejemplo en el caso de las flores, la anchura del pétalo de Iris Virgínica oscila entre 1,4 cm y 2,5 cm mientras que la de Iris Versicolor va desde los 0,1 cm hasta los 1,8. En este caso hay un pequeño solapamiento en el cual el modelo tendrá difícil saber de qué especie se trata, pero en el resto del dataset será realivamente fácil clasificar una u otra variedad.
Para encontrar la mejor solución, intentaremos cuantificar cada uno de estos enfoques. Con la tarjeta de crédito, tenemos un 100% de probabilidad de tener dinero para pagar otros gastos importantes. Pero la probabilidad de que paguemos el préstamo completamente se reduce significativamente. Los beneficios de este enfoque son que tendremos dinero disponible para otros gastos importantes. Por otra parte con la tarjeta de débito, tenemos una probabilidad cercana a cero de tener dinero para otros gastos importantes. Sin embargo, en este caso, la probabilidad de tener que reembolsar el préstamo no procede ya que no hemos pedido un préstamo. Los dos enfoques que acabamos de discutir son bastante extremos y, por lo general, hay un término medio
Pero si pagamos la mitad a crédito y el resto con el saldo de la tarjeta de débito tenemos un enfoque mixto en el cual podemos tener un 90% de éxito en ambas variables. Esto sería una representación más precisa de escenarios del mundo real para la mayoría de las personas. Donde, no hay certeza sobre un pago de un préstamo. Pero siempre hay una probabilidad asociada.
Si vemos este problema particular desde el punto de vista de un acreedor. El acreedor está haciendo los préstamos. Necesita planificar sus finanzas de acuerdo con la probabilidad de incumplimiento de cada uno de sus clientes.
El problema que enfrenta el acreedor que emite un préstamo es de regresión logística. Para representarlo gráficamente a lo largo del eje X, traza el retraso en el pago de cada cliente en número de días y en el eje Y se utiliza para estimar la probabilidad de que el cliente no pague su préstamo. Cada uno de estos ejes responde a diferentes preguntas. A lo largo del eje X, la pregunta que debe hacerse es ¿cuántos días más tiene el cliente para liquidar el préstamo antes de que se considere que está en mora? Y a lo largo del eje Y, obtenemos la respuesta a la pregunta, ¿cuál es la probabilidad de que el cliente incumpla el pago?
Esta relación se puede mapear trazando una curva en S. Esto se debe a que el plazo de amortización es binario. Una vez que hayamos cruzado la fecha límite, habremos perdido la oportunidad de pagar y definitivamente se nos considera morosos. Esta es la razón por la que la curva en S se aplana al final después de que se alcanza la fecha límite de reembolso. El valor mínimo de esta curva en S es 0, mientras que el techo es 1, lo que representa un rango de probabilidades. Esto contrasta con la regresión lineal, donde el rango de valores de y normalmente va desde menos infinito hasta más infinito.
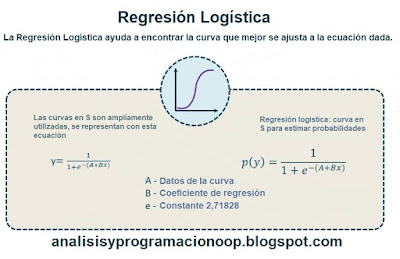
La curva en S ayuda al acreedor a responder a la pregunta de cuál es la probabilidad de que el cliente liquide su préstamo a tiempo. La solución al problema de la regresión logística es encontrar la curva de mejor ajuste para representar nuestros datos. Por tanto, las curvas en S se utilizan mucho y están representadas por esta ecuación:
y = 1 / (1 + e ^ - (A
+ Bx))
Para nuestro ejemplo de reembolso de préstamo, la probabilidad de incumplimiento se puede representar mediante esta curva en forma de S.
Donde en el rango de valores de x va desde de menos infinito a 0, la probabilidad es 0. Mientras que, la probabilidad es 1 para cualquier valor positivo de x. Por otro lado, cuando
tanto A como B son negativos, la regresión logística nos ayuda a comprender cómo las probabilidades de ciertos resultados se ven afectadas por las acciones.
Cuando echamos un vistazo a nuestra curva S, vemos que hay un valor mínimo para la probabilidad, que es 0. Esto está representado por todos los valores hacia la izquierda de este gráfico. Si un cliente tiene solo unos días para pagar, significa que es más probable que solo esté esperando el momento adecuado para pagar. Y la probabilidad de incumplimiento se puede considerar 0 en este rango en particular. Sin embargo, en el otro extremo de la escala, tenemos clientes que están muy cerca de su fecha límite o la han excedido. Y su probabilidad de incumplimiento puede considerarse 1. Sin embargo, entre estos dos extremos se encuentra la sección más interesante.
Y aquí es donde incluso un pequeño cambio en el valor de x puede resultar en un cambio significativo en el valor de y. De hecho, esta es una representación muy precisa de cómo se desarrollan las cosas en el mundo real. En la región verde del gráfico, la probabilidad de incumplimiento es muy sensible a cualquier retraso en el pago. Para ilustrar esto, consideremos dos clientes diferentes que realizan sus pagos los días X1 y X2. En comparación con otras secciones de este gráfico, la probabilidad de que estos clientes incumplan varía bastante en esta región.
Como acreedores, podemos trazar la curva S, que mapea la probabilidad de incumplimiento, de acuerdo con el retraso en el pago. Y después establecemos un valor de umbral a lo largo del eje X para el retraso del reembolso.
