Los autoencoders, al igual que otras redes neuronales pueden tener múltiples capas ocultas. En este caso los llamamos autoencoders apilados o autoencoders profundos. Añadir más capas ayuda al autoencoder a aprender codificaciones más complejas. Pero hay que ser cuidadoso de no implementar un autoencoder más potente de lo que necesitamos. Imaginamos por ejemplo un codificador tan potente que es capaz de mapear cada número individual de forma arbitraria y un decodificar que hace el mapeo inverso. Obviamente tal autoencoder debería ser capaz de reconstruir los datos de entrenamiento perfectamente, pero no sería capaz de aprender ninguna representación útil de los datos en el proceso (y esto no es útil para generalización de nuevas instancias).
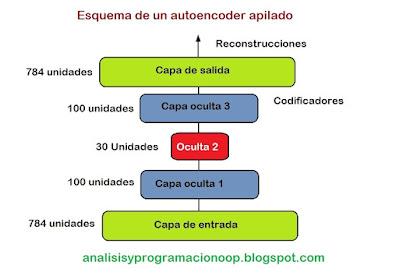
La arquitectura de un autoencoder apilado es tipicamente simétrica con respecto a la capa oculta central (la capa de codificación). Por ejemplo para codificar el dataset de moda MINST
Debería tener 784 entradas seguidas por una capa oculta de 100 neuronas , luego una capa central de 30 neuronas y otra capa oculta de 100 neuronas, finalmente una capa de salida de 784 salidas.
Vamos a construir un autoencoder apilado para trabajar con el dataset MNIST, utilizaremos activación SELU.
Cargamos el dataset MNIST
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full.astype(np.float32) / 255
X_test = X_test.astype(np.float32) / 255
X_train, X_valid = X_train_full[:-5000], X_train_full[-5000:]
y_train, y_valid = y_train_full[:-5000], y_train_full[-5000:]
Construimos un Autoencoder apilado con 3 capas ocultas y 1 capa de salida (es decir, 2 Autoencoders apilados).
def rounded_accuracy(y_true, y_pred):
return
keras.metrics.binary_accuracy(tf.round(y_true), tf.round(y_pred))
tf.random.set_seed(42)
np.random.seed(42)
stacked_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation="selu"),
keras.layers.Dense(30, activation="selu"),
])
stacked_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation="selu", input_shape=[30]),
keras.layers.Dense(28 * 28, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
stacked_ae = keras.models.Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1.5), metrics=[rounded_accuracy])
history = stacked_ae.fit(X_train, X_train, epochs=20,
validation_data=(X_valid,
X_valid))
Echemos un vistazo al código: el modelo de autoencoder se divide en dos submodelos, el codificador y el decodificador.
El codificador toma imágenes en escala de grises de 28x28 pixels, las aplana de tal forma que cada imagen es metida en un vector de 784 posiciones, entonces procesa tales vectores a través de dos capas densas de tamaños que van disminuyendo (primero a 100 unidades y después a 30), ambas capas utilizan la función de activación SELU. Para cada imagen de entrada, el codificador genera un vector de 30 posiciones.
El decodificador toma este vector de 30 posiciones (que es la salida del codificador) y lo procesa a través de dos capas densas incrementando sus tañamos desde 100 unidades hasta 784 y reconstruye el vector final como una imagen de escala de grises de 28x28 pixels con lo que la salida tiene el mismo tamaño que la entrada del codificador.
Cuando compilamos el autoencoder apilado utilizamos pérdida de entropía cruzada binaria en vez del error cuadrático medio. Estamos tratando esta tarea de reconstrucción como un problema de clasificación binaria múltiple: cada intensidad de pixel representa la probabilidad de que el pixel sea negro. Enmarcando este problema más bien como un problema de regresión, lo que hace que el modelo tienda a converger más rápidamente.
Finalmente entrenamos el modelo utilizando X_train como entradas y como objetivos, y similarmente utilizamos X_valid como entradas de validación y como objetivos.
Visualizando las reconstrucciones
Una forma de asegurarnos de que en autoencoder es entrenado apropiadamente es comparar las entradas con las salidas. Las diferencias no deberían ser demasiado significativas. Vamos a mostrar algunas imágenes de entrada junto con sus correspondientes salidas.
def show_reconstructions(model, images=X_valid, n_images=5):
reconstructions = model.predict(images[:n_images])
fig = plt.figure(figsize=(n_images * 1.5, 3))
for image_index in range(n_images):
plt.subplot(2, n_images, 1 + image_index)
plot_image(images[image_index])
plt.subplot(2, n_images, 1 + n_images + image_index)
plot_image(reconstructions[image_index])
show_reconstructions(stacked_ae)
save_fig("reconstruction_plot")
Las recostrucciones son reconocibles pero con un poco de pérdida. Necesitamos un entrenamiento más largo para el modelo o construir un codificador-decodificador más profundo. Pero tenemos una red neuronal bastante potente, podemos gestionarla para hacer reconstrucciones perfectas sin que aprenda ningún patrón útil en los datos.
Visualizando el dataset de moda MNIST
Ahora que hemos entrenado nuestro autoencoder apilado, podemos utilizarlo para reducir la dimensionalidad del dataset. Para visualización no devolverá grandes resultados comparado con otros algoritmos de reducción de dimensionalidad, pero una de las grandes ventajas de los autoencoders es que pueden manejar datasets grandes con muchas instancias y muchas características. De este modo, una estrategia es utilizar un autoencoder para reducir la dimensionalidad hasta un nivel razonable, y entonces utilizar otro algoritmo de reducción de dimensionalidad para visualización. Utilizaremos esta estrategia para visualizar el dataset de moda MNIST. Primero utilizaremos el codificador de nuestro autoencoder apilado para reducir la dimensionalidad por debajo de 30, y luego utilizaremos la implementación de Scikit-Learn de un algoritmo t-SNE para reducir la dimensionalidad a 2 para visualizarlo.
np.random.seed(42)
from sklearn.manifold import TSNE
X_valid_compressed = stacked_encoder.predict(X_valid)
tsne = TSNE()
X_valid_2D = tsne.fit_transform(X_valid_compressed)
X_valid_2D = (X_valid_2D - X_valid_2D.min()) / (X_valid_2D.max() - X_valid_2D.min())
plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap="tab10")
plt.axis("off")
plt.show()
El diagrama no es muy bonito, si queremos hacer un poco más vistoso hacemos:
# adaptado de
https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html
plt.figure(figsize=(10, 8))
cmap = plt.cm.tab10
plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap=cmap)
image_positions = np.array([[1., 1.]])
for index, position in enumerate(X_valid_2D):
dist = np.sum((position - image_positions) ** 2, axis=1)
if np.min(dist) > 0.02: # si está más lejos de otras imágenes
image_positions = np.r_[image_positions, [position]]
imagebox = mpl.offsetbox.AnnotationBbox(
mpl.offsetbox.OffsetImage(X_valid[index], cmap="binary"),
position, bboxprops={"edgecolor": cmap(y_valid[index]), "lw": 2})
plt.gca().add_artist(imagebox)
plt.axis("off")
save_fig("visualizacion_mnist_moda")
plt.show()
Esto devuelve como resultado un gráfico más amplio y con algunas imágenes como ejemplo. El algoritmo t-SNE identifica varios grupos razonablemente bien, representa cada clase con un color diferente.
De este modo los autoencoders pueden ser utilizados para reducción de dimensionalidad. Otra aplicación es para preentrenamientp no supervisado.Traducido del capítulo 17 de “Hands-On Machine Learning with Scikit-Learn, Keras and Tensorflow, 2nd Edition by Aurelien Géron (O’Reilly). Copyright 2019 Kiwisoft S.A.S., 978-1-492-03264-9”