Análisis de componentes principales PCA
Cuando tenemos varias características en nuestro conjunto de datos que están fuertemente correlacionadas entre sí. Y no está claro cuál de estas características es, de hecho, el mejor predictor del resultado que estamos tratando de predecir. Entonces podemos emplear la técnica del análisis de componentes principales. El análisis de componentes principales, o PCA, se puede definir como un procedimiento matemático, el cual puede transformar un número de variables correlacionadas en un número menor de variables no correlacionadas que se denominan componentes principales. Cuando se pasa de una gran cantidad de dimensiones (columnas con datos) a una menor cantidad de componentes principales. Lo que se ha efectuado se llama reducción de dimensionalidad. A continuación veremos un ejemplo de cómo funciona esto usando scikit-learn. Para aplicar el análisis de componentes principales, invocamos la clase PCA desde el módulo decomposition scikit-learn.
from
sklearn.decomposition import
PCA
pca
= PCA (n_components
= 3,
whiten = True)
Podemos inicializar este modelo PCA pasando algunos parámetros. Primero, especificamos el número de componentes principales que necesitamos usar. Nuestros datos de entrada originales contienen ocho características. Y reduciremos esto a un total de tres (por ejemplo) componentes principales. El parámetro whiten se usa para asegurar salidas no correlacionadas, y lo configuramos como True.
Ajustamos este modelo PCA con nuestros datos de entrenamiento.
x_reduced
= pca.fit_transform(X)
Hacemos uso del método fit_transform. Y pasamos todos los datos X que contienen todos los valores escalados para nuestras características de entrada.
El valor devuelto por fit_transform incluirá los tres componentes principales para cada uno de los puntos de datos en nuestro conjunto de datos. Por tanto, esta variable se denominará x_reduced. Una vez que nuestro modelo PCA se ha ajustado a nuestros datos de entrada, podemos hacer uso de su campo explained_variance_. Para ver la cantidad de variación que se explica por cada uno de los componentes principales.
pca.explained_variance_
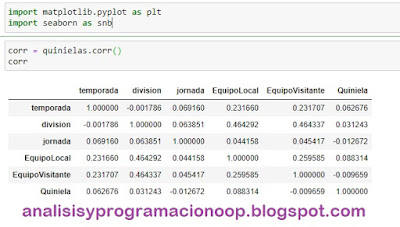
Lo que obtenemos aquí es una matriz, y podemos ver que el primer componente principal explica buena parte de la varianza. Aunque el resto de componentes también tienen valores próximos.
En vez de mirar estos números de varianza sin procesar, podemos hacer uso del campo explained_variance_ratio en el modelo PCA. Para ver qué proporción de la varianza subyacente es capturada por cada uno de los componentes principales.
pca.explained_variance_ratio_
Una vez lo que ejecutemos, obtenemos una matriz más y podemos ver aquí que el primer componente principal de hecho explica aproximadamente el 17 % de la varianza total. Mientras que el último componente principal explica solo la mitad del 12% de la varianza. Hay que tener en cuenta aquí que cada uno de estos componentes principales está organizado en el orden de varianza explicada.
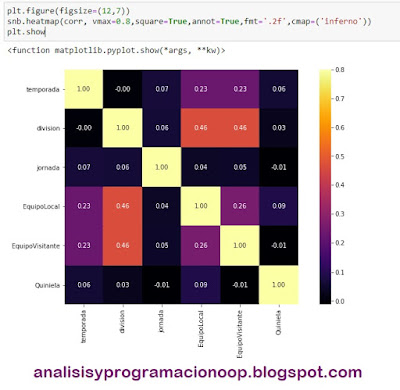
Una vez tenemos estos números de varianza, podemos generar un gráfico donde trazamos una línea para cada uno de los componentes principales y sus variaciones explicadas.Hacemos uso de la función de diagrama de Matplotlib, y luego le pasamos la matriz.
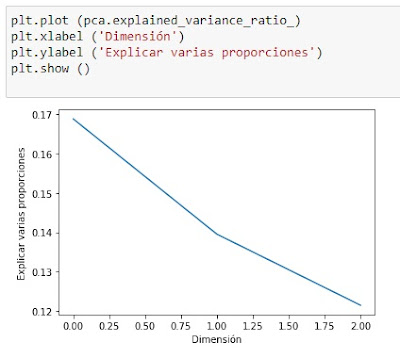
plt.plot (pca.explained_variance_ratio_)
Y formateamos el gráfico de modo que haya etiquetas para los ejes x e y.
plt.xlabel ('Dimensión')
plt.ylabel ('Explicar varias
proporciones')
plt.show ()
Ahora podemos visualizar muy claramente la caída en la varianza explicada para cada uno de los componentes principales. En este caso la caía no es muy significativa del primer componente principal al segundo ni del segundo al tercero.
Ahora que el modelo PCA ha reducido el tamaño de nuestros datos de entrada de un total de ocho columnas (o funciones o dimensiones) a tres componentes principales. Podemos construir un nuevo modelo de clasificación utilizando estos componentes principales.
x_train,
x_test, y_train,
y_test = train_test_split(x_reduced, Y,
test_size = 0.2,
random_state = 1)
Una vez más hemos hecho uso de la función train_test_split. Y en esta ocasión pasamos la variable x_reduced que contiene estos componentes principales en el lugar de la X. Todo lo demás es exactamente igual que antes, donde pasamos nuestras variables Y y especificamos un tamaño de conjunto de prueba del 20% del conjunto de datos.
Después inicializamos un clasificador de vectores de soporte. También en esta ocasión, no especificamos ningún parámetro para este clasificador y simplemente usamos los valores predeterminados.
svc_clf_pca
= SVC()
svc_clf_pca.fit(x_train, y_train)
Utilizaremos el método de ajuste del clasificador SVC para entrenar nuestro modelo. Y le pasamos las variables de entrenamiento x e y. En esta ocasión, el x_train contiene las tres componentes principales en lugar de ocho. Después de esto, nuestro entrenamiento del modelo está completo.
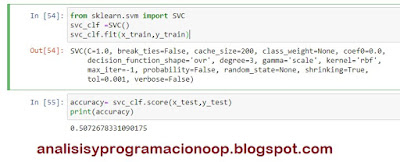
accuracy
= svc_clf_pca.score(x_test,
y_test)
print(accuracy)
¿Qué pasaría si redujéramos aún más el número de componentes principales?
pca
= PCA (n_components
= 2,
whiten = True)
incluso con dos componentes principales, todavía obtenemos una precisión de aproximadamente el 82%. (sobre 100%) vemos que no es tan preciso como tener tres componentes principales u ocho características de entrada.
Así que hemos visto cómo podemos reducir el número de dimensiones en nuestros datos de entrada y aun así obtener resultados muy precisos de nuestro modelo. Nuestro conjunto de datos solo contenía unos miles de filas. Si tuviéramos muchos más la precisión debería mejorar aún más.
Normalizar un conjunto de datos (dataset)
Anteriormente, usamos un escalar estándar para escalar todas las columnas de características en el conjunto de datos de resultados de los partidos para hacer una quiniela (hemos utilizado un dataset diferente; En la primera parte utilizamos una sola etiqueta de caracteres para representar 1,X,2 y ahora utilizamos tres columnas de etiquetas binarias, Q1; 1 para 1 y 0 para el resto, QX; 1 para la X y 0 para el resto y Q2; 1 para el 2 y 0 para el resto, lo mismo para los resultados del quinigol que representan los valores del quinigol; QGC0 ; 1 si el equipo local mete cero goles y 0 para el resto, QGC1; 1 si mete un gol, QGCM; 1 si mete más de dos goles, ídem para el visitante.
Después aplicamos la técnica de análisis de componentes principales, con el fin de reducir el número de dimensiones en nuestros datos de entrada. A continuación utilizaremos un normalizador en lugar de un escalador estándar en nuestras funciones de entrada y veremos cómo afecta esto a la precisión de nuestro modelo. Comenzamos importando la clase Normalizer de la biblioteca de preprocesamiento scikit-learn. Y también importamos la biblioteca NumPy.
import
numpy as np
from
sklearn.preprocessing import
Normalizer
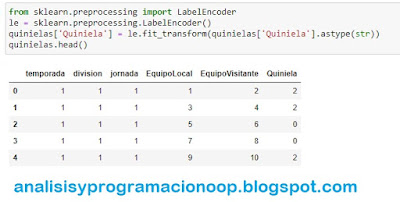
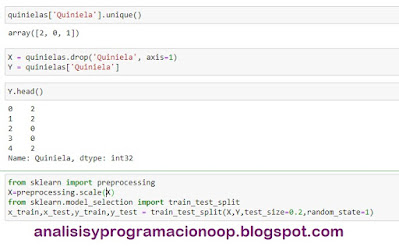
vemos cómo se ve el conjunto de datos de quinielas. Eliminamos todas las columnas de etiquetas.
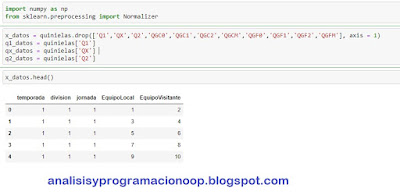
x_datos = quinielas.drop(['Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM'], axis = 1)
q1_datos = quinielas['Q1']
qx_datos = quinielas['QX']
q2_datos = quinielas['Q2']
x_datos.head()
Aquí vemos que el dataset contiene cinco características y once etiquetas (que hemos eliminado), que son las columnas que comienzan por Q. Nos quedamos con las cinco características o columnas después de eliminar las columnas de etiquetas.
Para aplicar el normalizador en nuestras columnas de características, ahora redefiniremos nuestros datos x e y.
Los datos x incluirán las columnas en nuestro Dataset de quinielas sin las etiquetas (las columnas de quinielas que empiezan por Q). Hemos utilizado la función drop para eliminarlas. Los datos y, solo incluyen las columnas de etiquetas, en este caso Q1, QX y Q2 para simplificar, aunque podríamos haber incluido las otras.
Antes de aplicar el normalizador a nuestros datos de entrada, necesitamos transformarlo en una matriz NumPy. Para hacer eso, podemos hacer uso del campo de valores de este Dataset. cuando ejecutamos la celda, nos queda una matriz de valores.
array = x_datos.values
array
Podemos ver su contenido. Vemos que tiene todos los datos en las celdas del Dataset. A continuación, aplicamos el normalizador a estos datos, lo inicializamos con los valores predeterminados. Y luego, utilizamos el método de ajuste del normalizador, al que alimentamos con la matriz que contiene todos los datos de características de nuestro conjunto de datos de quinielas.
scaler = Normalizer().fit(array)
scaler
El normalizador trabajará en cada una de las filas de nuestro conjunto de datos de forma independiente. Es decir, trabaja sobre una base transversal en lugar de una base longitudinal. Una vez que ejecutamos esta celda, nos queda un normalizador, que se ha ajustado a todos nuestros datos de entrada.
Podemos ver este normalizador. Y vemos los parámetros con los que se ha inicializado.
Confirmamos estos parámetros examinando el método get_params.
scaler.get_params
Transformamos el contenido de la matriz de entrada haciendo uso del método de transformación del normalizador.
Normalized_array = scaler.transform(array)
Esto tendrá el efecto de normalizar todas las características de nuestro conjunto de datos en cada fila de forma individual. Podemos echar un vistazo a cómo se ve este conjunto de datos normalizado. Y dado que todos los valores estarán entre 0 y 1 y se extenderán a múltiples dígitos más allá del punto decimal, estableceremos un valor de precisión de 3, utilizando el método set_printoptions de NumPy. Después, imprimiremos las primeras cinco filas de nuestra matriz normalizada.
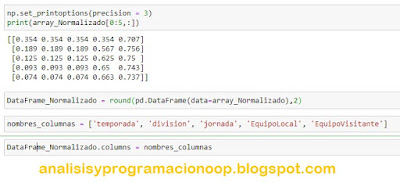
np.set_printoptions(precision
= 3)
print(array_Normalizado[0:5,:])
Podemos usar estos datos normalizados para construir un modelo de clasificación. Sin embargo, antes de esto, necesitaremos cargar el contenido en un DataFrame de pandas. Y si queremos redondear el contenido de todo el DataFrame a dos lugares decimales, podemos hacer uso de la función de redondeo aquí, donde el primer argumento es el DataFrame completo.
DataFrame_Normalizado
= round(pd.DataFrame(data=array_Normalizado),2)
Después de esto, podemos establecer los encabezados de columna para este DataFrame que acabamos de crear.
nombres_columnas = ['temporada', 'division', 'jornada', 'EquipoLocal', 'EquipoVisitante']
Estos son los mismos encabezados de columna que existían en el Dataset original. Para asignar estos encabezados de columna al DataFrame que hemos creado, podemos establecer el campo de columnas de ese DataFrame en esta lista de columnas que acabamos de crear.
DataFrame_Normalizado.columns = nombres_columnas
Ahora que tenemos todas las características normalizadas dentro de un DataFrame, podemos considerar combinar las características normalizadas con las etiquetas correspondientes. Para que tengamos ambas funciones y las etiquetas dentro del mismo DataFrame. Podemos hacer uso de la función pandas concat para eso.
DataFrame_Normalizado = pd.concat([DataFrame_Normalizado,q1_datos,qx_datos,q2_datos], axis = 1)
DataFrame_Normalizado.head()
Ahora podemos ver todas las características normalizadas y a qué etiquetas corresponden. Pasamos a definir nuestros datos de entrenamiento y prueba. Pero antes definiremos variables separadas para nuestros datos x e y. Los datos x incluirán todas las características normalizadas, mientras que los datos y solo incluirán las columnas de las etiquetas de nuestro DataFrame.
X = DataFrame_Normalizado.drop(['Q1','QX','Q2'], axis=1)
Y1 = DataFrame_Normalizado['Q1']
YX = DataFrame_Normalizado['QX']
Y2 = DataFrame_Normalizado['Q2']
Después de esto, dividimos los datos en conjuntos de prueba y de entrenamiento usando la función train_test_split una vez más.
x_train,x_test,y1_train,y1_test
= train_test_split(X,Y1,test_size=0.2,random_state=1)
x_train,x_test,yx_train,yx_test
= train_test_split(X,YX,test_size=0.2,random_state=1)
x_train,x_test,y2_train,y2_test
= train_test_split(X,Y2,test_size=0.2,random_state=1)
Definimos el clasificador de vectores de soporte lineal SVC. Una vez que inicializamos el clasificador, utilizando parámetros predeterminados, ajustaremos el clasificador a nuestros datos de entrenamiento.
svc_clf
= SVC()
svc_clf.fit(x_train,
y1_train)
Pasamos x_train e y1_train a este método de ajuste. Y en unos segundos, el modelo debería estar listo. Ahora podemos comenzar a evaluar este modelo. Y para eso, utilizamos el método de puntuación del clasificador, con el fin de verificar la precisión de las predicciones de este modelo con los datos de prueba.
svc_clf.fit(x_train,
y1_train)
accuracy
= svc_clf.score(x_test,
y1_test)
print (accuracy)
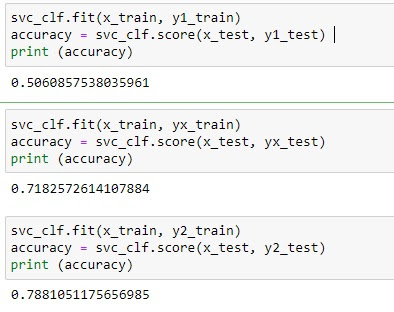
svc_clf.fit(x_train, yx_train)
accuracy
= svc_clf.score(x_test, yx_test)
print (accuracy)
svc_clf.fit(x_train, y2_train)
accuracy
= svc_clf.score(x_test, y2_test)
print (accuracy)
Y lo que obtenemos es una precisión de aproximadamente el 50,6% para los unos. Así que no está mal, aunque no particularmente bueno. Para las X es del 71,8 cual está muy bien para las X. Pero mucho ojo, no nos llevemos a engaño con esto, en realidad esto una clasificación binaria, si tenemos en cuenta que sólo el 27% de los valores son X, el resto es el 73% (n realidad tenemos un 27% de X y un 73% de no X) por tanto un 72% de aciertos significa que el 72% de las veces acierta si no es X tanto como si es X. Es como decir que si siempre ponemos no X, acertaremos el 73% de las veces, lo cual no es un gran avance.
Lo mismo sucede con los doses, un 78,8 % para los 2 tampoco nos esclarece mucho pues es la misma probabilidad de acierto que si siempre ponemos no 2.
Un normalizador es una mejor opción cuando realizamos agrupaciones en clústeres o clasificación de texto. Y esto no es necesariamente un buen ajuste para el modelo de clasificación que estamos tratando de construir aquí.
Pero en esta ocasión pasaremos algunos parámetros. No entraremos en detalles de cada uno de estos parámetros. Pero hay que saber que podemos ajustar los parámetros de nuestro modelo, para ver si eso mejora su rendimiento al hacer predicciones. Con este modelo SVC inicializado, podemos entrenarlo ajustándolo a los datos de entrenamiento. Y ahora nuestro modelo SVC está listo.
x_train,x_test,y1_train,y1_test = train_test_split(X,Y1,test_size=0.2,random_state=0)
slv_clf_mod
= SVC(random_state=5,tol=1e-3, C=1)
slv_clf_mod.fit(x_train,y1_train)
accuracy
= slv_clf_mod.score(x_test,
y1_test)
print (accuracy)
Así que es hora de que examinemos su precisión con los datos de prueba con la reducción de tolerancia que hemos hecho, para ver si esto mejora la precisión.
Como podemos ver, para el 1, la precisión es del 56,8 % prácticamente igual que antes, incluso peor, lo cual nos indica que este cambio de tolerancia no beneficia nuestra precisión de aciertos en nuestro modelo.