Regresión logística y clasificación para Machine Learning IV. Preparación de datos

Estos post están pensados para que el lector realice las pruebas con sus propios Datasets, pues ya estoy harto de seguir ejemplos siguiendo las instrucciones para tratar un dataset previamente descargado de internet con datos que ni entendemos ni nos sirven de mucho. Creo que se aprende mucho más creando tu propio dataset y adaptando las instrucciones a tus necesidades en vez de ejecutar como un robot las instrucciones del script. 

Vamos a crear un modelo de clasificación utilizando los conocimientos que hemos visto sobre regresión logística,

RL1, RL2, RL3, y scikit-learn.

import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

from sklearn import linear_model,  preprocessing

from sklearn.linear_model import LogisticRegression

Estas líneas llaman a las librería que necesitaremos. También vamos a suprimir las advertencias en el notebook, ya que algunas de las bibliotecas dependientes de scikit-learn pueden emitir advertencias.

import warnings

warnings.filterwarnings('ignore')

 import pandas as pd

quinielas = pd.read_csv('Completo_Etiquetado_Puntuado.csv') #tiene goles quiniela y quinigol

quinielas.head()

Una vez que hayamos cargado el conjunto de datos en el DataFrame, podemos mezclarlo haciendo uso de la función de muestra Pandas DataFrame. Y le especificamos una fracción de 1, de modo que se mezcle todo el conjunto de datos.

quinielas = quinielas.sample(frac = 1).reset_index(drop = True)

En nuestro caso no sería necesario hacer esto, pues ya son datos suficientemente aleatorios, pero con otro tipo de dataset puede venir bien hacerlo. Después, verificamos la longitud de este DataFrame en particular y obtenemos la información de que contiene 37147 filas de datos.

len(quinielas)

Si nuestra columna de etiquetas viene como cadena texto, es necesario realizar una codificación nuestro DataFrame.

No podemos usar valores de cadena cuando se introducen en nuestro modelo y debemos convertirlo en etiquetas específicas. Después de importar LabelEncoder, que es una de las herramientas de preprocesamiento de scikit-learn, lo aplicaremos a nuestra columna de etiquetas del DataFrame, usando la función fit_transform de LabelEncoder.

from sklearn.preprocessing import LabelEncoder

lb_make = LabelEncoder()

quinielas["etiqueta"] = lb_make.fit_transform(quinielas["etiqueta"])

En nuestro dataset tampoco es necesario pues todos estos pasos ya se siguieron en este curso pero dejo el código por si alguien lo necesita.

Esto reemplaza los valores actuales usados en la columna de la etiqueta con los valores codificados. 

Este conjunto de datos (dataset) incluye actualmente un total de 16 columnas, incluyendo la etiqueta. Lo que significa que hay 15 características potenciales que se pueden incorporar a nuestro modelo. Si tuviéramos que usar esas 15 columnas como características, esa técnica se denominaría regresión del sumidero de la cocina (kitchen sink regression). Ya que literalmente estamos utilizando todo en nuestro modelo. Sin embargo, estos modelos tienden a sobreajustarse (overfitting) con los datos de entrenamiento. Y terminan haciendo predicciones deficientes cuando se usan con datos reales. Una cosa que podemos hacer para evitar tal escenario es ser selectivos en las características que se utilizan para nuestro modelo. Es decir, realizamos una selección de funciones. Y para eso, usaremos un mapa de calor de Seaborn.

import seaborn as sns

import matplotlib.pyplot as plt

corrmat = quinielas.corr()

f,ax = plt.subplots(figsize = (15,15))

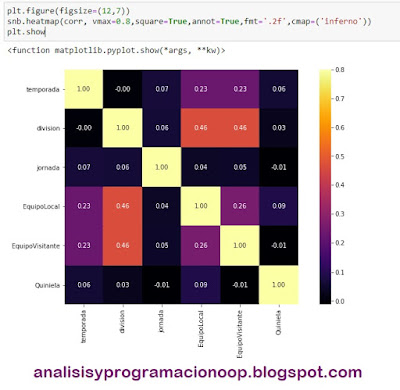
sns.heatmap(corrmat, vmax=.8, square=True, annot=True, fmt='.2f')

plt.show()

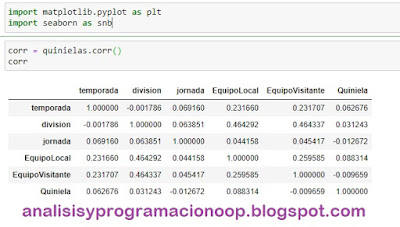
Importamos la biblioteca Seaborn y pyplot de matplotlib. Un mapa de calor tiene varios usos. Pero uno de ellos es visualizar la correlación entre varias columnas en nuestro  DataFrame. Si dos columnas están muy fuertemente correlacionadas entre sí, no tiene mucho sentido incluir ambas como características para nuestro modelo. Y probablemente podamos conformarnos con solo una. Para obtener toda la correlación entre las distintas columnas, usamos la función corr de Pandas.

Esto devolverá una matriz de correlación, que incluye los valores de correlación entre todos los posibles pares de columnas en nuestro DataFrame. Después, introducimos esta matriz de correlación en un mapa de calor de Seaborn, lo que nos facilitará la visualización de las correlaciones. Lo que nos permitirá identificar rápidamente qué columnas están fuertemente correlacionadas y potencialmente pueden eliminarse de nuestro conjunto de funciones. Inmediatamente algunas cosas saltan a la vista.

Los valores cercanos a 1 nos indicarán que no necesitamos una de esas dos columnas correlacionadas. En el mapa aparecen con tonos más claros en este mapa de calor en particular representan una correlación positiva muy alta, y los más oscuros representan correlaciones negativas muy altas. Después de analizar este mapa de calor, podemos llegar a las características que usaremos para nuestro modelo. Hay que tener en cuenta que la gráfica es simétrica por la diagonal, así que sólo tenemos que fijarnos en la parte inferior o en la superior pero no en ambas. En este caso elegimos la parte inferior. Otra cosa a destacar la he marcado en amarillo. Vemos una fuerte correlación entre los goles metidos por el equipo local cuando son más de 2 y por el visitante cuando se queda a 0, con el número de goles respectivo. Es lógico, las cuatro columnas son etiquetas y no aparecerán cuando pretendamos hacer predicciones. ¡ya quisiéramos saber los goles que va a meter cada equipo antes de hacer una quiniela!.

En este caso concreto lo que nos interesa son los equipos, junto con los puntos de cada equipo, su diferencia y sobre todo la diferencia de puntos normalizada, de cara a predecir el resultado de cada partido.

#quito todas las etiquetas excepto la Q1

#quito todos los puntos y dejo sólo la diferencia normalizada

x_data = quinielas.drop(columns = ['idPartido','temporada','golesLocal','golesVisitante','fecha','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM'])

x_data.head()

Así que hemos reducido de 15 columnas potenciales a 10 para rellenar nuestro x_data. Ahora configuramos nuestro y_data para que sea la columna de etiqueta de nuestro DataFrame.

y_data = quinielas ['Q1']

Y lo siguiente que hacemos es convertir los datos x e y en matrices NumPy.

import numpy as np

x_data = np.array(x_data)

y_data = np.array(y_data)

Una vez que se han convertido en matrices NumPy, podemos dividir nuestros datos x e y en conjuntos de prueba y de entrenamiento.

Debemos asegurarnos de que no estemos sobreajustado a los datos de entrenamiento, para lo cual creamos el conjunto de prueba por separado. Y aunque la división se puede realizar de varias maneras, usamos el 80% de los datos para entrenamiento y reservamos el 20% restante para propósitos de prueba. Una vez que nuestro x_data se ha dividido, también debemos aplicar una división correspondiente para y_data.

train_data = x_data[:29718]

test_data = x_data[29718:]

train_labels = y_data [:29718]

test_labels = y_data [29718:]

Dado que nuestro conjunto de datos contiene un total de 37147 filas, nuestros datos de entrenamiento incluyen todas menos las últimas 7429 filas que se convierten en nuestros datos de prueba. Y con eso, todos los datos que necesitamos para construir nuestro modelo de regresión lineal ya están listos.

Clasificación mediante un modelo de regresión logística

Ahora que hemos preparado todos los datos que necesitamos entrenar y evaluar nuestro modelo.

Hemos inicializado nuestro modelo de regresión logística con todos los parámetros predeterminados. Y después comenzamos el entrenamiento de este modelo llamándolo con la función de ajuste.

logisticRegr = LogisticRegression()

Para eso, analizamos todos nuestros datos x, es decir, los datos de entrenamiento, así como las etiquetas de entrenamiento. Esta formación debería ser razonablemente rápida, ya que no tenemos demasiadas filas de datos. Y una vez hecho esto, veremos que  hemos creado nuestro modelo de regresión logística y podemos echar un vistazo a todos los parámetros predeterminados para este modelo.

logisticRegr.fit(train_data, train_labels)

Entonces, ¿es correcto este modelo de regresión logística? solo hay una

forma de averiguarlo, y es usar test_data para obtener las predicciones.

predictions = logisticRegr.predict(test_data)

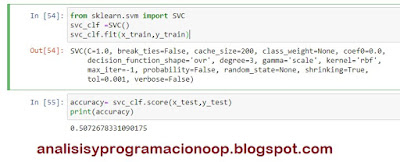
Para esto, hacemos uso de la función de predicción del modelo de regresión logística, a la que pasamos el test_data y obtenemos las predicciones. Podemos comparar los valores en estas predicciones con los valores reales y calcular una puntuación de precisión  nosotros mismos. O alternativamente, podemos hacer uso de la característica de puntuación de este modelo de regresión logística.

score = logisticRegr.score(test_data, test_labels)

print(score)

Para esto, alimentamos test_data y test_labels. Esto calculará las predicciones usando test_data y nuestro modelo de regresión logística y luego las comparará con test_labels para dar una puntuación de precisión. Y aquí vemos que nuestro modelo de regresión logística ha funcionado razonablemente bien, incluso con los parámetros predeterminados al obtener una puntuación de precisión del 50%. Lo que pone de manifiesto que se trata de datos estrictamente aleatorios.

Manejo de Conjuntos de datos (Datasets) para Machine Learning I

 Cargar y escalar un conjunto de datos  (Dataset)

En este post vamos a ver cómo tratar un conjunto de datos (dataset)  desde el principio para tratarlo con algoritmos de Machine Learning. Partiremos con un archivo .csv (valores separados por comas) que es bastante común en ML, todas sus columnas ya están con valores numéricos, excepto las etiquetas que son cadenas de caracteres.

Vamos a crear un modelo de clasificación utilizando la biblioteca scikit-learn y el lenguaje Python 3 sobre un cuaderno de notas de Jupyter. Primero, desactivaremos las advertencias. Pues es posible que aparezcan algunas advertencias debido a que las bibliotecas que usaremos a su vez tienen dependencias de otras bibliotecas que pueden quedar obsoletas.

import warnings

warnings.filterwarnings('ignore')

Importamos la biblioteca pandas que utilizaremos para cargar los datos de un archivo CSV en un Dataset de pandas. 

import pandas as pd

quinielas = pd.read_csv('Escalar_Dataset_Curso.csv')

Estamos cargando este archivo 'Escalar_Dataset_Curso.csv' en un conjunto de datos (dataset) y esto se hace usando la función read_csv en pandas.

Podemos obtener una vista previa de su contenido usando la función head.

quinielas.head()

Y lo que contiene este conjunto de datos es información sobre los resultados de los partidos. La idea es predecir el resultado adaptado a las quinielas, 1, X o 2. Los nombres de los equipos ya se han traducido a datos numéricos.

Las características del dataset incluyen representaciones numéricas excepto en las etiquetas. Las etiquetas de este conjunto de datos incluyen el resultado del partido en formato 1, X, 2. Hay algunas columnas que posiblemente no las necesitemos para construir un buen modelo de clasificación.

Antes de comenzar examinaremos el conjunto de datos comenzando con el número total de registros. Para esto, usaremos la función le, y vemos que en nuestro caso particular tenemos 36147 registros con los que trabajar.

quinielas.le

Recortaremos algunas características de este conjunto de datos, con lo que haremos uso de la función drop de pandas.

Así por ejemplo el IdPartido no es relevante para el resultado, entonces, como argumento, especificamos todas las columnas del dataset que deben eliminarse, y especificamos estas nueve columnas aquí. Aunque parezca contraproducente, hay que eliminar también las columnas de los resultados de los partidos, pues lo que realmente nos interesa es obtener el valor de la quiniela, 1,X, 2 y si no eliminamos esa información, el modelo será capaz de ‘prececir’ el 100% de los valores 1, X, 2  basándose en el número de goles de cada y lo que queremos es predecir estos valores antes del partido, es decir, antes de conocer los goles.

La guía real para predecir la quiniela, serán entonces las etiquetas, 1, X,2 de resultados pasados y el código del equipo que juega. El modelo deberá establecer que equipos tienen más o menos probabilidades de ganar, perder o empatar contra otros equipos.

quinielas.drop(['idPartido','golesLocal','golesVisitante'],axis = 1, inplace = True)

quinielas.head()

Para asegurarnos de que son las columnas las que se eliminan, especificamos que el argumento para el eje es = 1. Y al establecer el argumento inplace a True, el conjunto de datos (dataset) original se modificará con las columnas eliminadas. Podemos  examinar las primeras cinco filas usando la función head una vez más.

 

Y lo que nos queda son seis columnas en total. Estas incluyen las cinco columnas de características, y la etiqueta al final que es la llamada Quiniela. Podemos ver los  diferentes valores de las etiquetas 1,X y 2. Todas las columnas de este conjunto de datos en particular son numéricas. Pero los valores de la etiqueta (Quiniela) están en forma de cadenas de caracteres. Los algoritmos de aprendizaje automático no pueden trabajar con estos datos de cadena directamente, por lo que necesitaremos transformar esta columna de Quiniela en forma numérica. Esto es lo que haremos al codificar la etiqueta de la columna de clase.

Para eso, importaremos la clase LabelEncoder de la biblioteca de preprocesamiento scikit-learn. Y luego inicializaremos este LabelEncoder con todos los valores predeterminados para no definir explícitamente ningún parámetro. A continuación, para etiquetar y codificar la columna de clase de nuestro dataset simplemente lo pasaremos como un argumento con el método de transformación de ajuste de LabelEncoder.

import sklearn

from sklearn.preprocessing import LabelEncoder

le = sklearn.preprocessing.LabelEncoder()

#quinielas['Quiniela'] = le.fit_transform(quinielas['Quiniela'].astype(str))

quinielas.head()

 

Hay que tener en cuenta que estamos lanzando las etiquetas originales como tipo cadena. 

LabelEncoder necesita trabajar con tipos de cadenas para realizar una codificación. Una vez hemos codificado la etiqueta de la columna de clase de nuestro dataset, obtenemos una vista previa de su contenido una vez más. Podemos ver que la columna Quiniela contiene números en lugar de los valores de cadena originales. 

Este resultado muestra que hay tres clases diferentes de resultado de Quiniela, el 1, X, 2 se ha traducido por 0,1,2 en el nuevo conjunto de datos. Esto, nos da un punto de referencia para el modelo de clasificación. Si tuviéramos que hacer conjeturas aleatorias para cada resultado, deberíamos esperar obtener una precisión de 33% dado que hay tres opciones diferentes. Nuestro modelo debe funcionar significativamente mejor que esto al hacer sus predicciones. También hay que tener en cuenta que los datos no son completamente aleatorios, con lo que en realidad la distribución de las frecuencias en el dataset vienen del siguiente modo: la del 1 es del 51%, la de la X del 27% y la del 2 del 22%

quinielas['Quiniela'].unique()

Nos devuelve la lista de valores que se han asignado a las etiquetas, en nuestro caso, 0,1y 2.

Ahora que todas las características, están en el formato correcto, podemos definir las variables X e Y para nuestro conjunto de datos.

X = quinielas.drop('Quiniela', axis=1)

Y =  quinielas['Quiniela']

Así que definimos las variables X como todas las columnas del dataset de quinielas  excepto la columna con la Quiniela (la etiqueta), razón por la que hemos utilizado la instrucción drop. Estas serán todas nuestras características de entrada.

Definimos una variable Y como la columna de las etiquetas, en nuestro caso Quiniela. Así que ahora tenemos cinco funciones de entrada que representan varios detalles sobre las quinielas. Y estos se utilizarán para predecir un valor de Y que representa el resultado final.

Ahora que nuestro conjunto de datos se ha preparado y todas nuestras características de entrada son valores numéricos continuos, podemos seguir adelante y escalar todas estas características de entrada. Para eso, hacemos uso del módulo de preprocesamiento en la biblioteca scikit-learn, y luego hacemos uso de su función de escala para escalar todas nuestras características de entrada.

from sklearn import preprocessing

X=preprocessing.scale(X)

from sklearn.model_selection import train_test_split

El escalar que se utilizará para realizar esto será el escalar estándar. El escalar estándar tendrá el efecto de ajustar los valores en cada una de las columnas del dataset de manera independiente, de modo que cada distribución tenga una media cero y una unidad de varianza y desviación estándar. Y una vez que hayamos escalado todas las características de entrada, dividiremos nuestro conjunto de datos en conjuntos de prueba y de entrenamiento. Para eso, hacemos uso de la función de división de prueba de entrenamiento disponible en la biblioteca scikit-learn.

x_train, x_test,y_train,y_test = train_test_split(X,Y,test_size=0.2,random_state=1)

Los argumentos que le pasamos incluyen todas nuestras características de entrada de escala, esta es la variable Y. También podemos especificar el tamaño de nuestro conjunto de entrenamiento. Vemos que el 20% del conjunto de datos debe usarse para pruebas y el 80% restante se usará con fines de entrenamiento. Los datos de entrenamiento y prueba estarán disponibles en las variables x_train, x_test, y_train e y_test. Con todos los datos de prueba y entrenamiento listos, podemos seguir adelante y construir nuestro modelo de clasificación.

Detectando correlaciones en un conjunto de datos (dataset)

Hemos preparado previamente nuestro conjunto de datos de quinielas, de modo que contenga cinco características de entrada que son valores numéricos continuos. Luego pasamos a realizar un escalado estándar para estandarizar esas variables continuas. Y también etiquetamos y codificamos la columna de Quiniela de nuestro dataset. A continuación, hemos dividido nuestro conjunto de datos en componentes de entrenamiento y prueba, donde los datos de entrenamiento son el 80% del conjunto de datos y el 20% se utilizará para las pruebas. Ahora podemos usar esos datos para construir un modelo de clasificación.

Para entrenar este clasificador. Para ello le pasaremos nuestros datos de entrenamiento, las variables x_train e y_train. Estos datos de entrenamiento se pasan al método de ajuste del clasificador de vectores de soporte.

from sklearn.svm import SVC

svc_clf =SVC()

svc_clf.fit(x_train,y_train)

Una vez que el modelo está listo, podemos comenzar a evaluarlo con los datos de prueba.

accuracy= svc_clf.score(x_test,y_test)

print(accuracy)

Para eso, utilizamos la función score a la que pasamos las variables _test, que son las características de entrada de los datos de prueba, así como los valores reales de las etiquetas en los datos de prueba. La variable x_test que contiene todas las características de entrada será utilizada por el clasificador de vectores de soporte para hacer predicciones. Estas predicciones luego se compararán con la variable y_test, que contiene todos los valores reales. El valor devuelto por la función de puntuación (score) será la precisión del modelo. ¿Cuántas predicciones coincidieron realmente con los valores reales?

La precisión que obtenemos aquí es de 0.50 o aproximadamente 50%. Cuando se considera que había tres clases, las suposiciones a ciegas nos habrían dado una precisión de aproximadamente del 33%, pero al tener una parte predecible nos da una precisión del 50% en este caso es, de hecho, un rendimiento bastante mediocre, pues es lo que acierta cualquier persona con ciertos criterios al hacer una quiniela.

Sin embargo, dado que hay varias columnas diferentes disponibles en nuestro conjunto de datos. Es posible que muchos de ellos estuvieran, de hecho, muy fuertemente correlacionados entre sí. Tener características altamente correlacionadas podría afectar el rendimiento del modelo al hacer predicciones sobre datos reales. Por eso siempre es bueno recortar las características que no son necesarias. Para comprobar si hay campos en nuestro conjunto de datos que estén muy correlacionados, podemos hacer uso de una matriz de correlación. Podemos visualizar las correlaciones utilizando un mapa de calor. Para este propósito, usaremos las bibliotecas de visualización de datos matplotlib y seaborn. Así que importamos el objeto matplotlib.pyplot, así como la biblioteca seaborn a nuestro cuaderno.

import matplotlib.pyplot as plt

import seaborn as snb

Hecho esto,  para ver los valores de correlación entre todas las características en nuestro marco de datos, podemos hacer uso de la función corr. Esto devolverá una matriz de correlación, donde cada una de las características de nuestro conjunto de datos se emparejará con cada una de las demás, y luego se mostrarán los valores de correlación correspondientes.

corr = quinielas.corr()

corr

Podemos ver exactamente cómo se ve esta matriz de correlación, y podemos ver todos los valores de correlación. De modo que tenemos todas las características representadas a lo largo de las filas y columnas. Cada una de las celdas representa los valores de correlación para los pares de características correspondientes representados en la fila y la columna. Los valores de correlación van de menos 1 a más 1. Un valor negativo implica una correlación negativa, donde el aumento de un valor corresponde a una disminución del otro. Un valor de correlación positivo sugiere que un aumento en el valor de una característica da como resultado un aumento en la otra también.

Un problema con esta matriz de correlación es que contiene muchos números y hace difícil juzgar qué par de características están altamente correlacionadas. Por esa razón, ahora generaremos un mapa de calor. En una matriz de correlación con colores que se utilizan para indicar el grado de correlación.

Generamos una figura matplotlib, y luego la función de mapa de calor, cuyos argumentos incluyen la propia matriz de correlación, así como una serie de argumentos para formatear el mapa de calor. Esto representará una matriz de correlación de una manera mucho más intuitiva. 

plt.figure(figsize=(12,7))

snb.heatmap(corr, vmax=0.8,square=True,annot=True,fmt='.2f',cmap=('inferno'))

plt.show

Los colores más claros, representan valores altamente correlacionados positivamente. Mientras que los colores oscuros representan valores correlacionados negativamente. También podemos ver los números de correlación dentro de cada una de las celdas. Y podemos ver claramente si hay una serie de características en nuestro conjunto de datos que están fuertemente correlacionadas. En nuestro caso apenas hay correlación (la diagonal no cuenta porque es la correlación de cada columna consigo misma) por que ya hemos eliminado del dataset los goles, que era la característica altamente correlacionada, pero si se nos hubiera escapado alguna columna , aquí la veríamos claramente. 

Si hubiéramos encontrado muchas características transmitiendo de hecho la misma información. No es necesario que los incluyéramos todos al crear nuestro modelo de aprendizaje automático. Una forma de manejar situaciones en las que tenemos características altamente correlacionadas es eliminar manualmente algunas de las columnas que están altamente correlacionadas con otras. Esta técnica, no es eficaz además en las características fuertemente correlacionadas, es posible que no esté del todo claro cuál de esas características tiene una fuerte relación de causa y efecto con el valor que estamos tratando de predecir.

En este caso, existe un grave riesgo de que terminemos eliminando la columna que explica en gran medida la variación subyacente en nuestros datos. Para evitarlo, podemos emplear la técnica de análisis de componentes principales que exploraremos en el siguiente post