Los árboles de decisión son algoritmos de Machine Learning utilizados para clasificación múltiple de datasets etiquetados.
Vamos a comenzar con ejemplos prácticos con nuestro propio dataset (y ahora si) esta es la técnica más adecuada para este dataset aunque ya lo hemos utilizado para explicar otros conceptos de Machine Learning.
Estos post están pensados para que el lector realice las pruebas con sus propios Datasets, pues muchas veces seguimos ejemplos con instrucciones para tratar un dataset previamente descargado de internet con datos que ni entendemos ni nos sirven de mucho. Creo que se aprende mucho más creando nuestro propio dataset y adaptando las instrucciones a nuestras necesidades en vez de ejecutar las instrucciones del script. Aquí, Como crear nuestro propio dataset
El dataset que utilizaré es uno con los resultados de partidos de fútbol con la intención de calcular la quiniela más adecuada.
Comenzaremos importando las librerías necesarias y nuestro dataset.
Estas son las inicializaciones de rigor
# Requiere Python ≥3.
import sys
assert sys.version_info >= (3, 5)
# Requiera Scikit-Learn ≥0.20
import sklearn
assert sklearn.__version__ >= "0.20"
# importaciones comunes
import numpy as np
import pandas as pd
import os
# para hacer la salida de este notebook estable
np.random.seed(42)
# Para generar imágenes y gráficos
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
Y ahora cargamos el dataset y comprobamos sus datos mostrando la cabecera
from sklearn.tree import DecisionTreeClassifier
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_2.csv') #tiene goles quiniela y quinigol
quinielas.head()
Podemos echar un vistazo a nuestro dataset para comprobar su estructura. Por ejemplo para ver las columnas hacemos
#Para echar un vistazo a nuestro dataset, nos muestra las columnas del
dataset
list(quinielas.keys())
Ahora asociamos el dataset al árbol de decisión, en la X le asignamos el dataset al que le eliminamos las columnas de etiquetas y las que no son relevantes o no están normalizadas.
A la ‘y’ le asignamos la etiqueta de las Q1 en este caso y creamos una variable llamada arbol_clasificador a la que asignamos nuestro árbol con la instrucción DecisionTreeClassifier entrenado con las variables X e y.
#las X contienen los datos relevantes para hacer predicciones quitamos todas las etiquetas
X = quinielas.drop(columns=['idPartido','temporada','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','quiniela_arbol_decision'])
#las Y son las etiquetas a predecir, en este caso quitamos todo excepto 'Q1','QX','Q2'
y = quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp','quiniela_arbol_decision'])
arbol_clasificador = DecisionTreeClassifier(max_depth=2, random_state=42)
arbol_clasificador.fit(X, y)
Una vez entrenado nuestro árbol, vamos a realizar una primera predicción, pera ello lo primero que hacemos es mostrar la X para ver en qué orden tenemos que introducir los datos y cuales hay que introducir y cuales no.
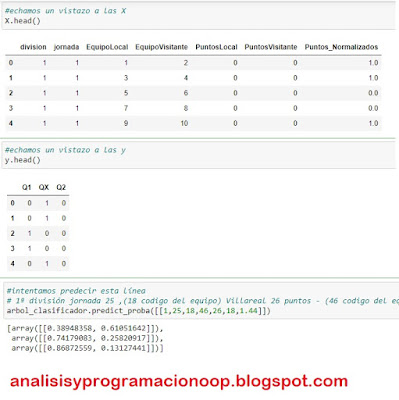
#echamos un vistazo a las X
X.head()
#echamos un vistazo a las y
y.head()
A continuación tomamos una línea al azar (en este caso la hemos cogido del dataset y probamos su predicción de probabilidades
#intentamos predecir esta línea
# 1ª división jornada 25 ,(18 codigo del equipo) Villareal 26 puntos -
(46 codigo del equipo) Levante 18 puntos 26/18 = 1,44
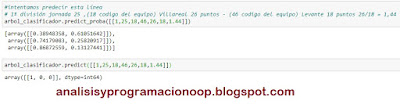
arbol_clasificador.predict_proba([[1,25,18,46,26,18,1.44]])
Y para ver los resultados que predice hacemos
arbol_clasificador.predict([[1,25,18,46,26,18,1.44]])
En este caso estamos intentando predecir la Q1, QX y Q2 y nos devuelve un array con la probabilidad de que sea no 1 (38,94 %) o 1 (61,05%), para la no X tenemos 74,17% frente a 25,82% de X y para el no 2 tenemos 86,87% frente al 13,12% de 2. (Nótese que primero predice la probabilidad de la negada, no del resultado) Como se puede ver, el array de resultados es [1,0,0] es decir 1. [0,1,0] sería X y [0,0,1] sería 2.
Árboles de decisión con Python
El conocimiento que un árbol de decisión adquiere a través del entrenamiento se expresa directamente como una estructura jerárquica. Y esta estructura retiene y muestra este conocimiento para que se entienda fácilmente. A continuación un ejemplo completo más sencillo que el anterior pero posiblemente más preciso.
Vamos a construir aquí un árbol de decisión.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import tree
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv') #tiene goles quiniela y quinigol
Echamos un vistazo al dataset con:
quinielas.head()
Y asociamos las X a los datos del Dataset y las Y a las etiquetas (en este caso sólo a Q1, QX y Q2)
#las X contienen los datos relevantes para hacer predicciones quitamos
todas las etiquetas
X = quinielas.drop(columns=['idPartido','temporada','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha'])
#las Y son las etiquetas a predecir, en este caso quitamos todo excepto
'Q1','QX','Q2'
y = quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp'])
Ahora dividimos el Dataset en una parte de entrenamiento y otra de testeo.
#Definimos la parte del Dataset que es de entrenamiento y la de testeo
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2, random_state=42)
Creamos una instancia para el árbol clasificador
Arbol_Clasificador
=
tree.DecisionTreeClassifier()
Y luego entrenamos el árbol de decisiones, pasándole X_train e y_train. Porque al igual que con otros clasificadores, DecisionTreeClassifier toma como entrada dos matrices, las matrices X e y.
Ahora creamos algunas predicciones. Primero entrenamos el árbol
Arbol_Clasificador =
Arbol_Clasificador.fit(X_train, y_train)
Y a continuación generamos las predicciones
#Evaluamos las predicciones con el subconjunto de testeo
Predicciones
= Arbol_Clasificador.predict(X_test)
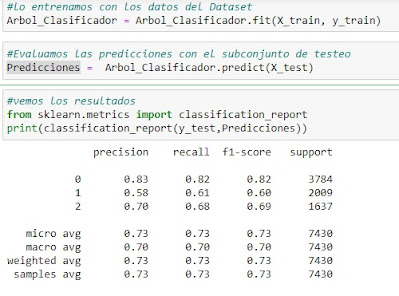
Y finalmente vemos los resultados
#vemos los resultados
from sklearn.metrics import
classification_report
print(classification_report(y_test,Predicciones))
En este caso 0 se corresponde con 1, 1 con X y 2 con el 2. Tenemos un 83% de aciertos para el 1, un 58% para la X y un 70 % para el dos lo cual no está nada mal.
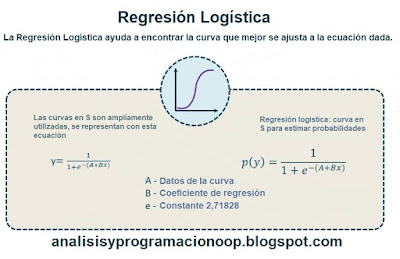
Árboles de Regresión
Los árboles de decisión también son capaces de ejecutar tareas de regresión. Como ejemplo, vamos a construir un árbol de regresión utilizando la clase DecisionTreeRegressor de la librería de Scikit-Learn y la vamos a entrenar con nuestro dataset para una profundidad máxima de 2 y de 3.
from sklearn.tree import
DecisionTreeRegressor
arbol_regresion_1 =
DecisionTreeRegressor(max_depth=2, random_state=42)
arbol_regresion_2 =
DecisionTreeRegressor(max_depth=3, random_state=42)
arbol_regresion_1.fit(X, y)
arbol_regresion_2.fit(X, y)
#intentamos predecir esta línea
# 1ª división jornada 25 ,(18 codigo del equipo) Villareal 26 puntos -
(46 codigo del equipo) Levante 18 puntos 26/18 = 1,44
arbol_regresion_1.predict([[1,25,18,46,26,18,1.44]])
arbol_regresion_2.predict([[1,25,18,46,26,18,1.44]])
En este caso sólo nos muestra la probabilidad del resultado, que es bastante cercana a la que vimos antes, en ambos caso es [1,0,0]
La diferencia entre un árbol de decisión y un árbol de regresión es que en el árbol de regresión en vez de tratar de predecir una clase en cada nodo, se predice un valor. Por ejemplo si queremos hacer una predicción para una nueva instancia, sea X= 1,444 comenzamos el árbol desde la raíz y alcanzamos una hoja nodo que predice el valor [1,0,0]. Esta predicción es el valor objetivo después de un entrenamiento de casi 2000 instancias asociadas a esta hoja del nodo.
Los árboles de regresión son propensos al sobreajuste, sobre todo cuando utilizamos los parámetros por defecto
Inestabilidad
Pero los árboles de decisión tienen mucho a su favor, son sencillos de comprender e interpretar, fáciles de usar, versátiles y potentes. Sin embargo tienen algunas limitaciones, por ejemplo sus límites de decisión son ortogonales (líneas rectas perpendiculares a los ejes) lo que les hace sensibles a la rotación. Este problema se puede tratar de solventar utilizando PCA
Pero el principal problema de los árboles de decisión es que son muy sensibles a pequeñas variaciones en los datos de entrenamiento, pues el cambio en un solo dato puede dar como resultado unos límites del árbol completamente diferentes.