Supongamos que preguntamos una cuestión difícil a miles de personas, si tomamos las respuestas del conjunto, podemos obtener una respuesta mejor que la de un experto. A este fenómeno se le llama sabiduría de la multitud. Del mismo modo si tenemos en cuenta las predicciones de un grupo amplio de predictores (tales como clasificadores o regresores) obtendremos mejores predicciones que con un solo predictor a este grupo de predictores lo llamamos conjunto (Ensemble) y a esta técnica la llamamos Aprendizaje por conjuntos (Ensemble Learning) y al algoritmo de aprendizaje por conjuntos lo llamamos Método de ensamblaje (Ensemble Method).
Un ejemplo de este método de ensamblaje consiste en el entrenamiento de un conjunto de árboles de decisión, lo que llamamos Bosque Aleatorio (Random Forest) a pesar de su simplicidad son uno de los métodos más potentes de Machine Learning de la actualidad.
Votando clasificadores
Vamos a suponer que entrenamos varios clasificadores y cada uno alcanza un 80% de precisión. Entre ellos tenemos uno por regresión logística, un SVM, un bosque aleatorio y algunos más. Una forma simple de mejorar nuestro clasificador para hacer predicciones consiste en hacer que cada uno de nuestros métodos realice una predicción y luego tomar la clase predicha por la mayoría. De modo que nuestro nuevo clasificador aumenta la precisión del mejor de cada uno de los predictores individuales.
Primero inicializamos nuestro script de Python.
# Requiere Python ≥3.
import sys
assert sys.version_info >= (3, 5)
# Requiera Scikit-Learn ≥0.20
import sklearn
assert sklearn.__version__ >= "0.20"
# importaciones comunes
import numpy as np
import pandas as pd
import os
# para hacer la salida de este notebook estable
np.random.seed(42)
# Para generar imágenes y gráficos
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
Cargamos el Dataset (es este caso es un dataset creado por mi) se pueden utilizar Datasets descargados de librerías, aunque recomiendo que cada uno trabaje con su propio dataset.
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv') #tiene goles quiniela y quinigol
quinielas.head()
from sklearn.model_selection import train_test_split
#las X contienen los datos relevantes para hacer predicciones quitamos
todas las etiquetas
X = quinielas.drop(columns=['idPartido','temporada','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha'])
#las Y son las etiquetas a predecir, en este caso quitamos todo excepto
'Q1','QX','Q2'
y = quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','Q1','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp'])
X_train,
X_test, y_train,
y_test = train_test_split(X, y,
random_state=42)
Dejamos las y como un array de una dimensión, esto nos dará advertencias, pero funciona, con tres dimensiones no funciona. En este caso dejamos que calcule las X de la quiniela (quitamos el Q1 y Q2).
Definimos un bosque aleatorio, un clasificador por votación, una regresión logística, y un SVM para evaluar que método acierta mejor las X de la quiniela.
from sklearn.ensemble import
RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import
LogisticRegression
from sklearn.svm import SVC
log_clf =
LogisticRegression(solver="lbfgs", random_state=42)
rnd_clf =
RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma="scale", random_state=42)
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='hard')
Entrenamos los diferentes métodos de clasificación
from sklearn.metrics import accuracy_score
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
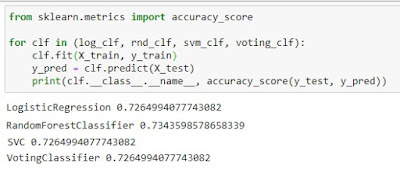
Y le indicamos que nos muestre el número de aciertos de cada método de cara a evaluar cual ha funcionado mejor.
from sklearn.metrics import accuracy_score
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__,
accuracy_score(y_test,
y_pred))
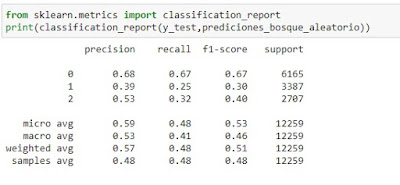
En este caso el bosque aleatorio es el que mejores resultados obtiene con un 73,44 %, aunque con un margen muy pequeño.
Si todos los clasificadores son capaces de estimar las probabilidades con el método predic_proba() podemos indicar a scikit-learn que muestre la clase con la probabilidad más alta, promediada sobre el resto de clasificadores individuales. Esto se llama soft voting. Y suele obtener mejores predicciones que hard voting porque asigna un mayor peso a los votos que obtienen mayores probabilidades. Para cambiar de hard voting a soft voting sólo tenemos que sustituir voting='hard' por voting='soft' Pero antes, debemos asegurarnos de que todos los clasificadores pueden estimar probabilidades. En este caso, tenemos SVC que no tiene ese método, de modo que necesitamos poner su hiperparámetro probability a True (esto hace que la clase SVC utilice validación cruzada para estimar las probabilidades de la clase).
log_clf =
LogisticRegression(solver="lbfgs", random_state=42)
rnd_clf =
RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma="scale", probability=True, random_state=42)
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='soft')
voting_clf.fit(X_train,
y_train)
Embolsado y pegado (Bagging and Pasting)
Acabamos de ver la forma de evaluar la precisión de diferentes clasificadores al mismo tiempo, para evaluar cual de ellos es el más adecuado para nuestro propósito. Otra aproximación consiste en utilizar el mismo algoritmo de entrenamiento pero entrenarlo en diferentes subsets aleatorios del set de entrenamiento, pero antes de hablar de embolsado y pegado, tenemos que saber qué es el Bootstrapping.
Bootstrapping, en estadística se refiere a un método de remuestreo que consiste en extraer repetidamente, con reemplazo, muestras de datos para formar otros conjuntos de datos más pequeños, llamados muestras de bootstrapping. Es como si el método bootstrapping estuviera haciendo un montón de simulaciones en nuestro conjunto de datos original, por lo que en algunos casos podemos generalizar la media y la desviación estándar.
Por ejemplo, digamos que tenemos un conjunto de observaciones: [2, 4, 32, 8, 16]. Si queremos que cada muestra de bootstrap contenga n observaciones, las siguientes son muestras válidas:
n = 3: [32, 4, 4], [8, 16, 2], [2, 2, 2]… Bagging
n = 3: [ 32, 4], [8, 16, 2], [2]… Pasting
Dado que extraemos datos con duplicidad, las observaciones pueden aparecer más de una vez en una sola muestra. Cuando las muestras permiten duplicidades, este método se llama Embolsado (Bagging) si se ejecutan sin duplicidad se llama pegado (Pasting).
Ambos, el embolsado y el pegado permiten entrenar instancias varias veces contra múltiples predictores pero sólo el embolsado permite entrenar instancias para ser muestreadas varias veces con el mismo predictor.
Una vez que todos los predictores son entrenados, el conjunto puede predecir una nueva instancia simplemente agregando la predicción de todos los predictores. La función de agregación es típicamente el modo estadístico (statistical mode) es decir, la predicción más frecuente (igual que el clasificador hard voting de antes) para clasificación, o media por regresión. Cada predictor individual tiene un sesgo más alto que si fuera entrenado por el conjunto original de entrenamiento, pero la agregación reduce ambos, el sesgo y la varianza. Generalmente el resultado final es que por conjuntos tenemos un sesgo similar pero una varianza menor que entrenando un predictor simple con el mismo conjunto de datos.
El código expuesto a continuación entrena un conjunto de 500 árboles de decisión clasificadores, cada uno de ellos entrenado con 100 instancias tomadas aleatoriamente de nuestro set de entrenamiento (con duplicados, pues es un ejemplo de Bagging, pero si queremos hacerlo pasting basta con poner en el código bootstrap =False). El parámetro n_jobs indica el número de CPU´s que utilizaremos, en este caso una.
from sklearn.ensemble import
BaggingClassifier
from sklearn.tree import
DecisionTreeClassifier
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
max_samples=100, bootstrap=True, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test,
y_pred))
BaggingClassifier automáticamente ejecuta soft voting en lugar de hard voting si el clasificador de base es capaz de estimar probabilidades, lo cual es el caso en los árboles de decisión.
Bosques aleatorios
Como se ha dicho al principio, un bosque aleatorio, consiste en un conjunto de árboles de decisión generalmente entrenados por el método Bagging (o algunas veces Pasting) típicamente indicando con max_samples el valor del set de entrenamiento. En vez de montar un BaggingClassifier y pasarle un DecisionTreeClassifier, en su lugar, podemos pasarle la clase RandomforestClassifier que es más conveniente y está más optimizada para los árboles de decisión (para tareas de regresión existe RandomforestRegressor)
from sklearn.ensemble import
RandomForestClassifier
rnd_clf =
RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf =
rnd_clf.predict(X_test)
Salvo algunas excepciones RandomForestClassifier tiene todos los parámetros de un árbol de decisión (pues se trata de varios árboles) más los hiperparámetros del propio control BaggingClassifier.
El algoritmo del bosque aleatorio introduce aleatoriedad extra cuando crecen los árboles; en vez de buscar la mejor característica cuando se divide un nodo, busca la mejor característica entre un subconjunto aleatorio de características. El algoritmo encuentra así una diversidad de árboles de los cuales toma los mejores, resultando así en un mayor rendimiento.
El siguiente clasificador BaggingClassifier es equivalente al mostrado más arriba.
bag_clf =
BaggingClassifier(
DecisionTreeClassifier(splitter="random", max_leaf_nodes=16, random_state=42),
n_estimators=500,
max_samples=1.0,
bootstrap=True, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred =
bag_clf.predict(X_test)
from sklearn.ensemble import
RandomForestClassifier
rnd_clf =
RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)
np.sum(y_pred
== y_pred_rf) / len(y_pred)
Otra cualidad que tienen los bosques aleatorios, es que hacen posible evaluar la importancia relativa de cada característica de nuestro conjunto de datos. Scikit-Learn calcula los resultados automáticamente. Podemos acceder a estos resultados con la variable feature_importance_
Impulsores (Boosting)
Se refiere a cualquier método de ensamblado que pueda combinar cualquier algoritmo de aprendizaje débil dentro de un algoritmo de aprendizaje más potente. La idea general consiste en entrenar secuencialmente los diferentes predictores de forma que cada uno trate de corregir a su predecesor. Hay muchos métodos de aprendizaje por boosting, pero el más popular de lejos es AdaBoost.
AdaBoost
Consiste en un clasificador (un árbol de decisión por ejemplo) que se entrena con un dataset y realiza predicciones sobre él. Entonces, sobre estas predicciones se fija en las que ha fallado, dándoles un mayor peso y ejecutando una nueva predicción con estos nuevos pesos. De modo que un segundo clasificador mejora algunos de estos fallos y aumenta el peso para los nuevos fallos de cara a entrenar un tercer clasificador y así sucesivamente.
Impulso de gradiente (Gradient Boosting)
Igual que AdaBoost, trabaja secuencialmente añadiendo predictores a un conjunto y cada uno corrigiendo a su predecesor. Sin embargo en vez de ajustar los pesos en cada iteración intenta mejorar el siguiente predictor con los errores residuales generados por el predictor anterior.
Apilado (Stacking)
El último método de conjuntos está basado en una idea simple, en vez de utilizar una función trivial para elegir cual es el mejor, se entrena un modelo para que lo calcule. El modelo se llama Blender (Batidora) por que toma como entradas las salidas de todos los predictores. Por desgracia, Scikit-Learn no tiene funciones para hacer apilado, aunque existen métodos para implementarlo fácilmente de forma manual.