Bosques aleatorios con Python (Random Forest)

El bosque aleatorio (Random Forest)  crea un bosque o un conjunto de árboles de decisión. Entrenados mediante el método de embolsado (Bagging). La ventaja conceptual de este método es que una combinación de modelos de aprendizaje debería mejorar el resultado general. Un bosque aleatorio crea varios árboles de decisión y luego los combina para obtener una predicción más precisa y un mejor resultado general.

Estos post están pensados para que el lector realice las pruebas con sus propios Datasets, pues no veo de mucha utilizad seguir ejemplos siguiendo las instrucciones para tratar un dataset previamente descargado de internet con datos que ni entendemos ni nos sirven de mucho. Creo que se aprende mucho más creando nuestro propio dataset y adaptando las instrucciones a nuestras necesidades en vez de ejecutar como un robot las instrucciones del script. 

Aquí tenemos como crear nuestro propio dataset 

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

import pandas as pd

quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv') #tiene goles quiniela y quinigol

from sklearn.model_selection import train_test_split

from sklearn import tree

from sklearn.ensemble import RandomForestClassifier

En las líneas de arriba hemos importado algunas librerías, nuestro Dataset y  un clasificador de bosque aleatorio de la librería de scikit-learn.

A continuación cargamos una variable ‘X’ con los datos de nuestro Dataset y una ‘y’ con las etiquetas. Y generamos un subconjunto de entrenamiento y otro de pruebas.

#las X contienen los datos relevantes para hacer predicciones quitamos todas las etiquetas

X = quinielas.drop(columns=['idPartido','temporada','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha'])

#las Y son las etiquetas a predecir, en este caso quitamos todo excepto 'Q1','QX','Q2'

y = quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp'])

 

#dividimos nuestros datos en un conjunto de entrenamiento y otro de pruebas

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33,random_state=42)    

Ahora, creamos una instancia del clasificador del árbol de decisiones, y la entrenamos con la intención de obtener algunas predicciones.

arbol_decision = tree.DecisionTreeClassifier()

arbol_decision = arbol_decision.fit(X_train, y_train)

prediccion_arbol_decision= arbol_decision.predict(X_test)

Creamos una instancia del clasificador de bosque aleatorio, estoy especificando el número de estimadores como 5, podemos variar eso como queramos. También entrenamos el bosque aleatorio.

Bosque_aleatorio = RandomForestClassifier(n_estimators=5)

Bosque_aleatorio.fit(X_train, y_train)

Hacemos algunas predicciones

prediciones_bosque_aleatorio = bosque_aleatorio.predict(X_test)

E imprimimos los resultados de la predicción del arbol de decisión primero.

from sklearn.metrics import classification_report

print(classification_report(y_test, prediccion_arbol_decision))

 

A continuación imprimimos los resultados del bosque aleatorio

from sklearn.metrics import classification_report

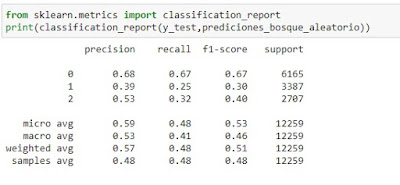
print(classification_report(y_test,prediciones_bosque_aleatorio))

 

Y los números son claramente inferiores en el bosque aleatorio. Lo cual resulta extraño, pues debería ser lo contrario, aunque tengo la impresión de que los aciertos del árbol de decisión no son realistas. En ambos casos, la tabla tiene los encabezados de columna: precisión, recuperación, puntuación f1 y soporte. Incluido un resumen al final.

Así que ahora y variamos el número de estimadores a 10. Cambiamos el valor de 5 a 10 en el código

Bosque_aleatorio = RandomForestClassifier(n_estimators=10)

También variaremos el tamaño de la prueba. Hagamos que el tamaño de la prueba sea del 60%. Eso significa que solo tendremos el 40% para entrenamiento, así que veremos si eso tiene un impacto.

#dividimos nuestros datos en un conjunto de entrenamiento y otro de pruebas

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.60,random_state=42)    

 

Aquí vemos que los resultados varían. En realidad no hay garantía de que el  bosque aleatorio supere al árbol de decisiones en todo momento. Entonces, ¿qué dice esto? los bosques aleatorios que constan de varios árboles individuales, cada uno basado en una muestra aleatoria de datos de entrenamiento, suelen ser más precisos que los árboles de decisión únicos. Los árboles de decisión únicos tienen árboles que se podan, mientras que los bosques aleatorios no se podan. Son diversos, simplemente tienen una resolución más alta en el espacio de funciones. Por lo que también tienden a manejar mejor el sobreajuste. De hecho, en la mayoría de los casos, encontraremos que los bosques aleatorios suelen ser más precisos que los árboles de decisión únicos.