En este post trataré de ofrecer una comprensión conceptual de cómo funcionará un modelo de regresión logística con Keras, pues Keras es muy utilizado para construir redes neuronales.
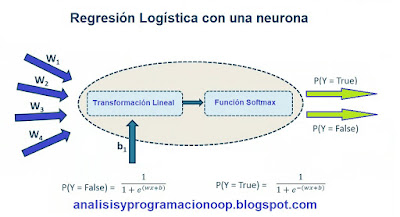
Antes de nada, veremos cómo se puede utilizar sólo una neurona para realizar una regresión lineal. Una vez que introducimos los datos de entrenamiento, la neurona realizará una transformación en la forma Y = Wx + b, que es la ecuación de una línea recta. El propósito de este entrenamiento es encontrar los valores óptimos de W (los pesos de la entrada) y b (el desplazamiento respecto al eje o sesgo [bias]), para minimizar la pérdida de datos de entrenamiento. Hecho esto, tenemos un modelo de regresión lineal con los valores óptimos de W y b. Esta es la red neuronal más simple posible, donde solo tenemos una neurona y esta realiza una transformación lineal simple. Si hacemos zoom en la neurona, vemos que hay una serie de entradas diferentes W. Dentro de la neurona hay dos funciones. Una de ellas es una transformación lineal y las entradas de esta, que serán las entradas de la propia neurona. La otra es la función de salida de dicha transformación lineal que alimenta una función de activación. El propósito de la función de activación es introducir un elemento de no linealidad en la salida de la neurona.
Esta no linealidad es necesaria para capturar relaciones más complejas entre la entrada y la salida, lo que se aplica a la mayoría de los casos de uso de redes neuronales. Sin embargo, si estamos utilizando una red neuronal de este tipo para hacer una regresión lineal, no necesitamos este componente no lineal en la neurona. Y podemos transmitir la transformación lineal con una función de identidad. Esto garantiza que la salida de la neurona sea, de hecho, la salida de la propia transformación lineal.
Función SoftMax
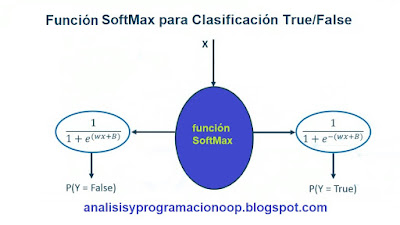
Para realizar una regresión logística, podemos reemplazar esta función de identidad por una función softmax. La función softmax asegura que la salida de nuestra neurona sea categórica. Es decir, si queremos que esta neurona realice una clasificación binaria, podemos configurar la función softmax para producir dos o n salidas. De esta forma, una vez que introducimos todas las entradas en esta neurona, la combinación de la transformación lineal y la función softmax producirá dos posibilidades de salida (activada y no activada o 1 y 0), que corresponde a las dos categorías distintas. También hay que tener en cuenta que nuestra transformación lineal incluirá un valor de sesgo además de los pesos de la entrada. La combinación de esta transformación lineal y la función softmax terminará produciendo una regresión logística. El resultado de esta regresión logística podría ser una probabilidad de que un evento en particular sea falso. Y la probabilidad de que el mismo evento sea cierto es simplemente 1 menos la probabilidad de que sea falso.
Si echamos un vistazo más cercano al componente softmax. Podemos decir que cualquier entrada x que entre en una función softmax, que esté configurada para generar valores verdaderos o falsos (true o false), producirá dos salidas distintas. Una que contiene la probabilidad de que el evento sea falso y la otra de que el evento sea verdadero.
La función softmax (también llamada exponencial normalizada) se puede ampliar para realizar la clasificación de N categorías. Cuando definimos una función softmax para nuestro modelo, podemos configurarla para generar N categorías diferentes en lugar de dos. La función softmax generará puntuaciones de probabilidad para cada categoría de salida. Y la categoría que tenga la mayor probabilidad se elegirá como predicción del modelo. Una vez hayamos configurado nuestra red neuronal poniendo en la última capa una salida softmax. La salida de nuestro modelo corresponderá al número de categorías diferentes que pueda tomar la salida. Y cada una de estas categorías estará asociada con una puntuación de probabilidad.
Esto se llama Regresión Logística Multinomial o Regresión Softmax. El clasificador por Regresión Softmax predice sólo una clase cada vez. Es decir, es multi-clase, no multi-salida. Por lo que debe ser utilizado solamente para clases mutuamente excluyentes, como el caso que hemos visto de las diferentes flores, pero no deberá ser utilizado por ejemplo, para reconocer a múltiples personas en un cuadro.
Una vez Softmax ha calculado la probabilidad de una instancia de pertenecer a cada clase, comparamos los resultados de salida con los datos reales, para ver lo acertados o fallidos que han sido. Y realimentar nuestro modelo para que mejore sus predicciones. Esta comparación se realiza con una función llamada Entropía Cruzada y trata de minimizar la llamada función de costo de la salida, que es el error cometido en cada predicción.
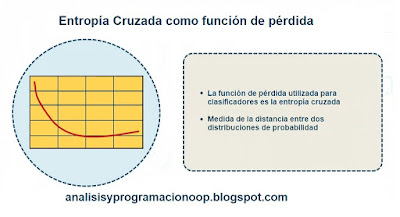
Entropía Cruzada
La Entropía Cruzada se originó a partir de la teoría de la información. Supongamos que queremos transmitir eficientemente todos los días la información del tiempo desde una estación hasta una emisora. Si tenemos ocho posibles tipos de tiempo. Soleado, nublado, nubes y claros, lluvioso, ventoso, etc necesitamos utilizar tres bites de información 2 elevado a 3= 8. Si embargo si la mayor parte del tiempo es soleado podemos ser más eficientes codificando soleado sólo con un bit (0) y las otras siete opciones con cuatro bits comenzando por 1 seguido de los tres bits restantes. La entropía cruzada mide el número medio de bits que enviamos realmente en cada opción. Si la estación meteorológica se encuentra en un desierto y asumimos que el tiempo es casi siempre soleado, la entropía cruzada será igual que la entropía del propio tiempo (intrínsecamente impredecible). Pero si hacemos una mala asunción (es decir en realidad, llueve con frecuencia) la entropía cruzada será grande.
Por otro lado, si las distribuciones de probabilidad reales están muy desincronizadas con las predicciones, lo que tenemos es un valor muy alto de entropía cruzada. En el caso de una regresión lineal, el objetivo sería minimizar el error cuadrático medio, que es una función de pérdida comúnmente utilizada. Pero en el caso de un modelo de clasificación, el objetivo es minimizar la entropía cruzada. Las funciones de entropía cruzada en la mayoría de las bibliotecas de aprendizaje automático realizarán algún tipo de estimación de las distribuciones de probabilidad de los valores reales.
Hasta ahora, los problemas de clasificación que hemos discutido simplemente han involucrado clasificación binaria, que es la forma más simple. Sin embargo, si nuestra salida debe tener N categorías diferentes, necesitamos alguna forma de manejar esto en un clasificador. Esto será especialmente útil para identificar letras o números manuscritos, o si nuestro modelo está destinado a clasificar imágenes.