Ya vimos algo de teoría sobre este tema. Podemos encontrar una buena tasa de aprendizaje entrenando nuestro modelo durante unos pocos cientos de iteraciones aumentando exponencialmente la tasa de aprendizaje desde un valor pequeño a uno muy grande y observando la tasa de aprendizaje mientras tomamos cada vez una tasa de aprendizaje ligeramente más pequeña y lo entrenamos de nuevo.
Pero podemos hacerlo mejor que con una tasa de aprendizaje constante: si comenzamos con una tasa de aprendizaje grande y la reducimos en cada iteración, tendremos un progreso más rápido.
Podemos ver diferentes técnicas y sus ejecuciones comparadas en este paper. Y también podemos consultar la técnica de programación de un ciclo ( 1 cycle Scheduling).
A continuación vamos a implementar algunas de estas técnicas con Keras.
Se muestra el proyecto completo igual que en entrada anterior , en gris el código y en color la parte necesaria para este ejemplo.
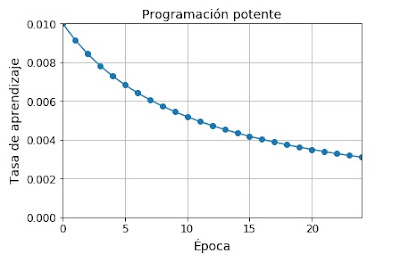
En el caso de la programación potente (Power scheduling) se puede implementar fácilmente con Keras simplemente con la línea
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
Esta línea inicializa el valor del hiperparámetro decay cuando creamos el optimizador. El hiperparámetro decay es la inversa de s (el número de pasos que resulta de dividir la tasa de aprendizaje por más de una unidad)
# Python ≥3.5
import sys
assert sys.version_info
>= (3, 5)
# Scikit-Learn ≥0.20
import sklearn
assert sklearn.__version__
>= "0.20"
try:
# %tensorflow_version solo existe en Colab.
%tensorflow_version 2.x
except Exception:
pass
# TensorFlow ≥2.0
import tensorflow as
tf
assert tf.__version__
>= "2.0"
# importaciones
comunes
import numpy as
np
import os
# para hacer este
cuaderno estable
np.random.seed(42)
import tensorflow as
tf
from
tensorflow import keras
#importamos nuestro
dataset
import pandas as
pd
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv')
#tiene goles quiniela y quinigol
quinielas.head()
#las X contienen los
datos relevantes para hacer predicciones quitamos todas las etiquetas
#dejamos división,
jornada, EquipoLocal, EquipoVisitante, PuntosLocal, PuntosVisitante,
Puntos_Normalizados
X = tf.cast(quinielas.drop(columns=['idPartido','temporada','golesLocal','golesVisitante','fecha','timestamp','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM']),
tf.float64)
#las Y son las
etiquetas a predecir, en este caso quitamos todo excepto 'Q1','QX','Q2'
y = tf.cast(quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp']),
tf.float64)
x_data = np.array(X)
y_data = np.array(y)
#dividimos el dataset
en una parte de entrenamiento y otra de testeo
train_data = x_data[:29718]
test_data = x_data[29718:]
train_labels = y_data [:29718]
test_labels = y_data [29718:]
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
# Normalización por
lotes antes de la función de activación
model = keras.models.Sequential([
keras.layers.BatchNormalization(),
keras.layers.Dense(300,
use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100,
use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(3,
activation="softmax")
])
model.compile(loss="categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
#entrenamos y evaluamos el modelo
n_epochs = 25
history = model.fit(train_data, train_labels, epochs=25,
validation_data=(test_data , test_labels))
# Para mostrar graficos
%matplotlib
inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
learning_rate = 0.01
decay = 1e-4
batch_size = 32
n_steps_per_epoch = len(train_data) // batch_size
epochs = np.arange(n_epochs)
lrs = learning_rate / (1 + decay * epochs *
n_steps_per_epoch)
plt.plot(epochs, lrs,
"o-")
plt.axis([0, n_epochs - 1, 0, 0.01])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Power Scheduling", fontsize=14)
plt.grid(True)
plt.show()
Para la programación exponencial (Exponential scheduling) es igual pero donde poníamos
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
ponemos:
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return
exponential_decay_fn
exponential_decay_fn
= exponential_decay(lr0=0.01, s=20)
Evitando el sobre-entrenamiento a través de la regularización
Las redes neuronales profundas pueden tener miles o incluso millones de parámetros, lo que nos brinda una increíble cantidad de libertad para entrenar una vasta variedad de conjuntos de datos. Pero esta gran cantidad de flexibilidad también convierte la red en propensa al sobre-entrenamiento. Necesitamos regularización.
Dropout
Dropout (Abandono) es una de la técnicas más populares de regularización para redes profundas explicada en este paper de 2012 y este de 2014
El dropout aumenta en un 1-2% la precisión de la red profunda. Puede que un 1 o 2% no nos parezca una mejora muy grande, pero si nuestra red ya tiene un 95% de precisión, aumentar al 97% implica una disminución del error cercana al 40% (del 5% al 3%).
Se trata de un algoritmo bastante sencillo, en cada paso de entrenamiento, cada neurona, incluyendo las neuronas de entrada, pero siempre excluyendo las neuronas de salida) tiene una probabilidad p de ser temporalmente “abandonada” lo que significa que es ignorada durante el paso de entrenamiento, pero debe ser activada en el siguiente paso. El parámetro p se llama tasa de abandono y está típicamente entre el 10 y el 50% siendo más cercana al 20-30% en las redes neuronales recurrentes y en torno al 40-50% en redes neuronales convolucionales. Después del entrenamiento las neurona no se abandonan más. En principio la técnica parece contraintuitiva, pero esta técnica hace que las neuronas no pueden adaptarse a lo que hagan sus neuronas vecinas, lo que las convierte en lo más útiles posible por si mismas, tampoco pueden confiar excesivamente en las neuronas de entrada por lo que deben poner atención en todas las neuronas de entrada en su conjunto. Al final, la red se hace menos sensible a cambios sutiles en las entradas y al final tenemos una red más robusta y que generaliza mejor.
Para implementar el dropout con Keras podemos utilizar la capa keras.layers.Dropout durante el entrenamiento elimina neuronas de la red de forma aleatoria (las pone a 0) y divide las entradas entre las neuronas restantes. Después del entrenamiento las entradas pasan a la siguiente capa. En este caso hemos tomado un dropout del 20%.
# Python ≥3.5
import sys
assert sys.version_info
>= (3, 5)
# Scikit-Learn ≥0.20
import sklearn
assert sklearn.__version__
>= "0.20"
try:
# %tensorflow_version solo existe en Colab.
%tensorflow_version 2.x
except Exception:
pass
# TensorFlow ≥2.0
import tensorflow as
tf
assert tf.__version__
>= "2.0"
# importaciones
comunes
import numpy as
np
import os
# para hacer este
cuaderno estable
np.random.seed(42)
import tensorflow as
tf
from
tensorflow import keras
#utilizamos la
inicialización He normal
keras.layers.Dense(10, activation="relu",
kernel_initializer="he_normal")
init = keras.initializers.VarianceScaling(scale=2.,
mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10, activation="relu",
kernel_initializer=init)
#importamos nuestro
dataset
import pandas as
pd
quinielas = pd.read_csv('Completo_Etiquetado_Puntuado_3.csv')
#tiene goles quiniela y quinigol
quinielas.head()
#las X contienen los
datos relevantes para hacer predicciones quitamos todas las etiquetas
#dejamos división,
jornada, EquipoLocal, EquipoVisitante, PuntosLocal, PuntosVisitante,
Puntos_Normalizados
X = tf.cast(quinielas.drop(columns=['idPartido','temporada','golesLocal','golesVisitante','fecha','timestamp','Q1','QX','Q2','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM']),
tf.float64)
#las Y son las
etiquetas a predecir, en este caso quitamos todo excepto 'Q1','QX','Q2'
y = tf.cast(quinielas.drop(columns=['division','jornada','idPartido','temporada','PuntosLocal','PuntosVisitante','EquipoLocal','Puntos_Normalizados','EquipoVisitante','QGC0','QGC1','QGC2','QGCM','QGF0','QGF1','QGF2','QGFM','timestamp','golesLocal','golesVisitante','fecha','timestamp']),
tf.float64)
x_data = np.array(X)
y_data = np.array(y)
#dividimos el dataset
en una parte de entrenamiento y otra de testeo
train_data = x_data[:29718]
test_data = x_data[29718:]
train_labels = y_data [:29718]
test_labels = y_data [29718:]
# Dropout
model = keras.models.Sequential([
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu",
kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(3, activation="softmax")
])
model.compile(loss="categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
#entrenamos y evaluamos el modelo para DROPOUT
n_epochs = 2
history = model.fit(train_data, train_labels, epochs=2,
validation_data=(test_data ,
test_labels))
Si observamos que el modelo sigue sobre-entrenado podemos incrementar la tasa de dropout (abandono) y a la inversa, si vemos que el modelo está sub-entrenado, podemos disminuir la tasa de dropout. También nos puede ser de utilidad aumentar las tasas de dropout en capas con muchas neuronas, y disminuirla en capas con pocas neuronas