Optimización de la velocidad de entrenamiento de redes neuronales

Entrenar una red neuronal profunda puede ser dolorosamente lento, aquí presentaremos cuatro formas de aumentar esta velocidad y alcanzar una solución mejor. 

Vamos a explorar los parámetros y enfoques esenciales para optimizar la velocidad de entrenamiento de las redes neuronales. Para optimizar la velocidad de entrenamiento de las redes neuronales, hay ciertas métricas que debemos vigilar y controlar según las iteraciones del aprendizaje. Necesitamos configurar los ajustes de diferentes hiperparámetros para lograr un rendimiento de aprendizaje óptimo de las redes neuronales. La primera es la función de pérdida. Que es una métrica o parámetro importante que se evalúa a nivel de lote durante el paso hacia adelante del proceso de aprendizaje.

La segunda métrica es la precisión del entrenamiento. Necesitamos rastrear y especificar esta métrica mientras entrenamos un clasificador. Y las métricas brindan la capacidad de identificar sobreajustes en los modelos de redes neuronales. La tercera es la proporción de pesos y sus actualizaciones. Necesitamos evaluar y rastrear los pesos para cada conjunto de parámetros, mutuamente excluyentes entre sí e impulsar el resultado dependiendo de cuán menor o mayor sea la proporción de peso más baja o más alta que la tasa de aprendizaje. Finalmente tenemos la actualización u optimización del momento en cada iteración resta el gradiente local del vector de momento (momento multiplicado por la tasa de aprendizaje) y actualiza los pesos sumando su vector de momento.

La métrica es la función de activación. Hay varias funciones de activación que gestionan la distribución de las activaciones neuronales entre el rango de menos uno y uno. 

Función de pérdida

Es una métrica importante que es útil para tener en cuenta durante el entrenamiento de una red neuronal, ya que se evalúa en cada época durante su entrenamiento.

 

El gráfico ilustra los efectos de diferentes tasas de aprendizaje. Las bajas tasas de aprendizaje proporcionarán mejoras lineales. Esto se ilustra con la curva de la línea naranja en el gráfico. Las tasas de aprendizaje muy altas proporcionarán mejoras exponenciales como lo indica la línea púrpura en el gráfico. Las altas tasas de aprendizaje ayudarán a disminuir la pérdida mucho más rápido. Pero existe el riesgo potencial de quedar atrapado en el peor valor de pérdida. 

Si consideramos la naturaleza general de la curva en el gráfico, observaremos que a medida que aumentamos el número de épocas mientras aplicamos diferentes tasas de aprendizaje, la función de pérdida tiende a disminuir. 

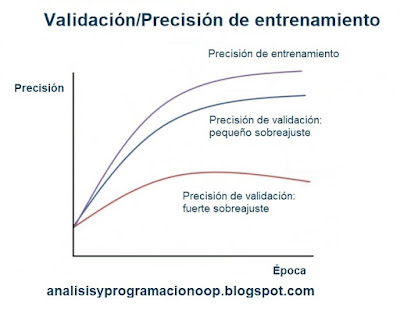
Precisión del entrenamiento

La precisión del entrenamiento puede afectar los escenarios de sobreajuste en nuestros modelos de redes neuronales.

 

En el gráfico vemos la brecha entre la precisión del entrenamiento y la validación, lo que muestra la cantidad de sobreajuste. Se proporcionan dos posibles escenarios de sobreajuste en el gráfico. El error de validación, indicado como la curva de color rojo en el gráfico, muestra una precisión de validación pequeña o marginal, en comparación con la precisión de entrenamiento, que se representa con la curva de color púrpura.

En tales casos, observaremos un fuerte sobreajuste. Y en otro para reducir el sobreajuste, podemos aumentar la regularización o recopilar más datos y ejecutar las épocas en consecuencia. El otro error de validación o curva de precisión, indicada como la curva de color azul en el gráfico, muestra una precisión de validación mejor o más alta en comparación con la misma precisión de entrenamiento que se muestra con la curva de color púrpura. En tales casos, observaremos un sobreajuste pequeño o débil, lo que a su vez indica que la capacidad del modelo de red puede no ser lo suficientemente alta.

Podemos aumentar la cantidad de parámetros para asegurarnos de obtener un modelo más grande. Siempre que calculamos el gradiente con retropropagación, generalmente usamos el gradiente para realizar actualizaciones de parámetros con el fin de optimizar las redes neuronales. Hay varios enfoques que podemos utilizar para actualizar los parámetros. El primer enfoque de este tipo es una actualización de momento.

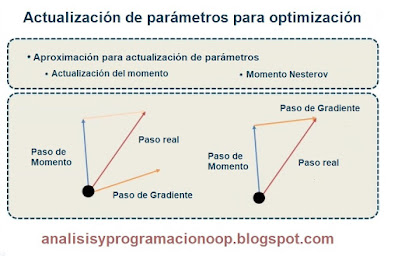
Actualización del momento 

La actualización del momento es un enfoque que proporciona una mejor convergencia que el descenso del gradiente estocástico porque calcula promedios de peso exponenciales que, a su vez, proporcionan una mejor estimación, que está más cerca de las derivadas reales. La figura de la ilustración en la parte inferior izquierda ilustra este enfoque al proporcionar una convergencia comparativa del paso de momento con el paso real y el paso de gradiente. El segundo enfoque que podemos utilizar para actualizar los parámetros es la actualización de momento de Nesterov, que es una versión modificada de la actualización de momento. Este método funciona un poco mejor que la actualización de momento. La figura de la ilustración de muestra en la parte inferior derecha muestra la actualización de momento de Nesterov. O también llamada Nesterov accelerated Gradient (NAG).

 

No estamos evaluando el gradiente en la posición actual, que se indica con un círculo o un punto negro. Sabemos que el momento nos llevará a la punta de la flecha de color azul. Por lo tanto, evaluamos el gradiente desde una posición mirando hacia adelante, que se indica con la flecha de color naranja. 

Uno de los enfoques esenciales para reducir la tasa de aprendizaje es el  decaimiento del paso (Step Decay), donde la tasa de aprendizaje se reduce en un cierto porcentaje después de completar un cierto número de épocas de entrenamiento. En otras palabras, la disminución de pasos reduce la tasa de aprendizaje en un cierto factor cada pocas épocas.

La reducción de la tasa de aprendizaje con decaimiento escalonado puede implicar dos enfoques diferentes. El primero es la caída exponencial, que disminuye a una tasa proporcional al valor actual. Se considera que cualquier cantidad que decae en un porcentaje fijo a intervalos regulares posee una caída exponencial. El segundo enfoque es la desintegración de 1/t. Este enfoque implica reducir la tasa de aprendizaje en función del número de iteraciones. El siguiente enfoque para la reducción de la tasa de aprendizaje implica la optimización de hiperparámetros. Sabemos que las redes neuronales generalmente involucran numerosos ajustes de hiperparámetros. Y algunos de los hiperparámetros más comunes en el contexto de las redes neuronales incluyen la tasa de aprendizaje inicial, el programa de disminución de la tasa de aprendizaje y la fuerza de regularización.

La tasa de aprendizaje inicial es un hiperparámetro configurable que generalmente usamos al entrenar redes neuronales. Es un valor positivo pequeño, a menudo en el rango de 0,0 y 1,0. El programa de disminución de la tasa de aprendizaje, también conocido como esquemas de disminución, puede implicar una disminución lineal hasta que alcancemos una tasa de aprendizaje mínima fija. La regularización se refiere al proceso de modificación de los algoritmos de aprendizaje para favorecer reglas de predicción más simples para evitar el sobreajuste. Podemos modificar la función de pérdida para penalizar determinados valores de los pesos que estamos aprendiendo mediante la regularización. Algunos ejemplos de fuerza de regularización incluyen penalización L2, fuerza de abandono, entre otros. 

Conjunto de modelos 

Es un enfoque confiable para mejorar el rendimiento de las redes neuronales, donde entrenamos múltiples modelos independientes y promediamos sus predicciones. Con el creciente número de modelos en el conjunto, el rendimiento mejorará gradualmente. Podemos formar un conjunto de modelos usando algunos enfoques distintivos. El primer enfoque es formar un conjunto con el mismo modelo, pero con diferente inicialización. Este enfoque implica una validación cruzada para determinar los mejores hiperparámetros que podemos usar para entrenar múltiples modelos, pero con diferentes inicializaciones aleatorias. El segundo enfoque es utilizar diferentes puntos de control de un solo modelo.

Este enfoque implica el uso de diferentes puntos de control de un solo modelo o red a lo largo del tiempo para formar un conjunto. El enfoque final es ejecutar el promedio de parámetros mientras se entrenan las redes neuronales. Y este enfoque implica promediar el estado de un modelo en múltiples iteraciones anteriores. Lo hacemos manteniendo una copia diferente de los pesos del modelo en la memoria que, a su vez, podemos usar para almacenar una suma exponencialmente decreciente de los pesos anteriores.