En esta entrada veremos el concepto y las características de los algoritmos evolutivos, los algoritmos genéticos y el descenso de gradiente.
El objetivo de implementar redes neuronales es lograr un aprendizaje optimizado de los modelos informáticos. La informática evolutiva es un grupo de algoritmos destinados a la optimización. Y están fuertemente inspirados por la evolución biológica. La idea fundamental detrás de la computación evolutiva es impulsar un conjunto de soluciones que se generen y actualicen de forma iterativa. Hay tres algoritmos esenciales que evolucionaron a partir de propiedades matemáticas y genéticas. Y comparten algunas características comunes que se derivan de la computación evolutiva. El primero es el algoritmo evolutivo, el segundo es el algoritmo genético y el tercero es el gradiente de descenso. El algoritmo evolutivo es esencialmente un algoritmo de optimización genérico basado en poblaciones, se utiliza de forma destacada para realizar aproximaciones de soluciones para los problemas identificados o dados. El algoritmo genético se considera uno de los algoritmos evolutivos más populares, que generalmente se usa para problemas de optimización, está inspirado en los principios biológicos de recombinación y mutación. El algoritmo de descenso de gradiente, es otro algoritmo de optimización esencial que se utiliza de forma destacada para minimizar las funciones de coste y actualizar los parámetros de los modelos de redes neuronales. Los parámetros pueden ser coeficientes para regresión lineal o pesos para redes neuronales.
Algoritmos evolutivos
Se considera un subconjunto de la computación evolutiva. Se implementan en sistemas informáticos y resuelven problemas incorporando las técnicas de algoritmo evolutivo, evolución diferencial, algoritmo genético y búsqueda. El algoritmo evolutivo utiliza ciertos mecanismos que se inspiran en la evolución biológica. La evolución biológica se refiere a cualquier cambio genético en una población que se hereda durante varias generaciones.
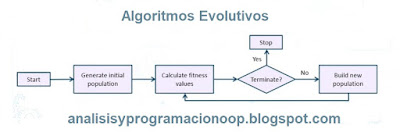
La imagen muestra el diagrama de flujo que involucra la implementación de algoritmos evolutivos. La implementación es un proceso iterativo y comenzamos generando la población inicial. Después de haber generado la población inicial, calcularemos los valores de aptitud.
Si hemos alcanzado la condición de optimización o el umbral de aptitud, finalizamos el proceso. De lo contrario, generaremos una nueva población, calcularemos la aptitud y evaluaremos hasta que hayamos alcanzado el umbral de valor de aptitud óptima o la condición de optimización.
Algoritmos genéticos
Se inspiran en el proceso de selección natural. Con la implementación de este algoritmo, seleccionamos una parte de la población existente de generaciones sucesivas para crear una nueva generación y luego aplicamos procesos basados en la aptitud.
Los algoritmos genéticos se utilizan para generar soluciones de alta calidad para manejar y gestionar problemas de optimización y búsqueda. Las soluciones se construyen utilizando funciones de aptitud que se definen sobre representaciones genéticas, lo que a su vez proporciona la capacidad de medir la calidad de las soluciones generadas. El algoritmo genético se basa en la teoría de la evolución propuesta por Charles Darwin. Un enfoque científico que explica y predice fenómenos que ocurren naturalmente en base a observaciones y experimentación.
La figura muestra el diagrama de flujo de la implementación de algoritmos genéticos. El proceso comienza con el muestreo de la población inicial. Después se aplica el proceso de selección, mejoramiento, cruce y transformación para generar una nueva población. Todo el proceso se repite hasta que hayamos obtenido una población correctamente ajustada.
Descenso de gradiente
Es otro algoritmo esencial que se utiliza con frecuencia en el aprendizaje automático y el aprendizaje profundo para optimizar los modelos. Es un algoritmo de optimización iterativo de primer orden que podemos usar para encontrar el mínimo de una función. El descenso de gradiente se puede implementar de forma iterativa para identificar los parámetros óptimos para los modelos. Se implementa ampliamente para derivar el mínimo local de una función y también se utiliza para entrenar redes neuronales.
Para optimizar los modelos y derivar el mínimo local de una función, el descenso de gradiente utiliza tres parámetros importantes. Estos parámetros incluyen ponderaciones, sesgos y función de costos. Para mejorar un conjunto dado de ponderaciones, obtenemos el valor de la función de costo para dichas ponderaciones y calculamos el gradiente. Después nos movemos en una dirección que reduzca la función de costo, Comenzamos inicializando los pesos al azar, luego calculamos el gradiente de la función de costo con respecto a los parámetros. Esto se hace mediante diferenciación parcial. Pues el valor del gradiente depende de la entrada, los valores actuales de los parámetros del modelo y de la función de costo. Después, se actualizan los pesos con valores proporcionales a los valores del gradiente.
E iteramos los primeros tres pasos hasta que los valores de la función de costo dejen de reducirse. Cuando estamos actualizando los pesos, implica una tasa de aprendizaje. Y esta tasa de aprendizaje determina el tamaño de los pasos que damos para alcanzar un mínimo. Debemos ser cautelosos al definir la tasa de aprendizaje. Una tasa de aprendizaje alta puede superar el mínimo y una tasa de apren