Construyendo una red neuronal de regresión utilizando la API Sequential de Keras

Vamos a utilizar la API Sequential de Keras para crear una red neuronal, secuencial, entrenarla y evaluarla. Podemos utilizar esta red neuronal de regresión para hacer predicciones. Para poder trabajar tendremos que importar las librerías de tensorflow, numpy y keras.

import tensorflow as tf

import numpy as np

from tensorflow import keras

Antes de nada para tener un dataset de ejemplo sobre el que trabajar vamos a descargar un dataset de Scikit-Learn llamado fetch_california_housing() con datos numéricos de inmuebles de California.

from sklearn.datasets import fetch_california_housing

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import StandardScaler

 

housing = fetch_california_housing()

 

X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)

X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)

 

scaler = StandardScaler()

X_train = scaler.fit_transform(X_train)

X_valid = scaler.transform(X_valid)

X_test = scaler.transform(X_test)

 

np.random.seed(42)

tf.random.set_seed(42)

Hacer predicciones con regresión es bastante similar a hacerlo con clasificación, una de las diferencias,  es el hecho de que la capa de salida es una única neurona (si sólo deseamos predecir un único valor), otra que  utilizamos la función de activación relu, y finalmente que la función de pérdida es el error cuadrático medio. Para este caso, como el dataset tiene bastante ruido, utilizaremos una capa oculta para evitar el sobreentrenamiento.

A continuación la creación de la red neuronal con la API de Keras.

model = keras.models.Sequential([

    keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),

    keras.layers.Dense(1)

])

model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))

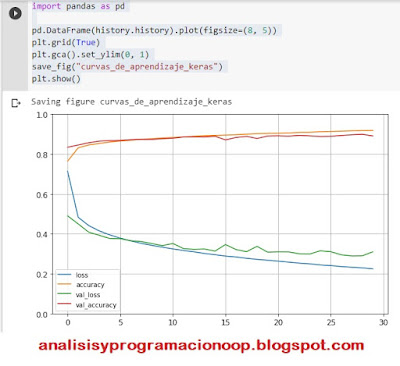
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))

mse_test = model.evaluate(X_test, y_test)

X_new = X_test[:3]

y_pred = model.predict(X_new)

Como podemos ver, la API Sequential es bastante fácil de utilizar, pero si queremos crear redes neuronales con topologías más complejas que la secuencial, podemos utilizar la API Functional.

Construyendo redes neuronales complejas utilizando la API Functional de Keras

En este caso construiremos una red neuronal con capas ocultas y un atajo de este estilo.

El código con la API de keras  será como este.

entrada = keras.layers.Input(shape=X_train.shape[1:])

oculta1 = keras.layers.Dense(30, activation="relu")(entrada)

oculta2 = keras.layers.Dense(30, activation="relu")(oculta1)

concat = keras.layers.concatenate([entrada, oculta2])

salida = keras.layers.Dense(1)(concat)

model = keras.models.Model(inputs=[entrada], outputs=[salida])

Podemos ver un esquema de la red neuronal creada

model.summary()

 

Veamos lo que significan las líneas de código

En primer lugar necesitamos crear un objeto entrada, lo creamos especificando el tipo de modelo que queremos, incluyendo su forma y su tipo.

Después creamos una capa oculta densa con 30 neuronas utilizando la activación ReLU y le pasamos su entrada como si fuera una función, en nuestro caso (entrada).

Creamos una segunda capa oculta y la usamos de nuevo como si fuera una función, pasandole la salida de la primera capa oculta.

Después creamos la capa concatenada y una vez más la usamos como si fuera una función, concatenando la entrada y la salida de la segunda capa oculta en los parámetros de la función.

Creamos la capa de salida con una única neurona y sin función de activación y la usamos como una función pasandole como parámetro la salida de la capa de concatenación.

Finalmente creamos el modelo Keras, especificando cuales son sus entradas y sus salidas.

Una vez creado el modelo procedemos como siempre, compilándolo,  evaluándolo y utilizándolo para hacer predicciones.

model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))

history = model.fit(X_train, y_train, epochs=20,

                    validation_data=(X_valid, y_valid))

mse_test = model.evaluate(X_test, y_test)

y_pred = model.predict(X_new)

Pero ¿Que sucede si lo que queremos es enviar un subset de datos por el atajo y el otro por el camino habitual? Tal y como se muestra en el esquema.

entrada_A = keras.layers.Input(shape=[5], name="atajo")

entrada_B = keras.layers.Input(shape=[6], name="profunda")

oculta1 = keras.layers.Dense(30, activation="relu")(entrada_B)

oculta2 = keras.layers.Dense(30, activation="relu")(oculta1)

concat = keras.layers.concatenate([entrada_A, oculta2])

salida = keras.layers.Dense(1, name="salida")(concat)

model = keras.models.Model(inputs=[entrada_A, entrada_B], outputs=[salida])

El código es muy similar al anterior, sólo  que ahora en las entradas hemos añadido entrada_A y entrada_B ahora vamos a compilarlo, pero en vez de pasarle una sola matriz de entrada X_train le pasaremos dos matrices, X_train_A y X_train_B, igual deberemos hacer con X_valid para la evaluación y X_text para la predcción.

model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))

 

X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]

X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]

X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]

X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]

 

history = model.fit((X_train_A, X_train_B), y_train, epochs=20,

                    validation_data=((X_valid_A, X_valid_B), y_valid))

mse_test = model.evaluate((X_test_A, X_test_B), y_test)

y_pred = model.predict((X_new_A, X_new_B))

 

Clasificador de imágenes con una red neuronal Keras

Ya hemos comentado aquí lo que es una red neuronal, ahora vamos a descargar el dataset MNIST  de prendas de ropa que contiene 60.000 imágenes de prendas de vestir en escala de grises de 28x28 pixels. El dataset contiene 10 categorías o clases de prendas de vestir. Previamente tendremos instalado en nuestro equipo un entorno virtual de Anaconda con Tensorflow instalado (enlace), o podemos optar también por ejecutar las instrucciones en la nube con Colaboratory.

Hecho esto importamos Tensorflow y Keras 

import tensorflow as tf

from tensorflow import keras

Cargamos el dataset de Moda de MNIST

fashion_mnist = keras.datasets.fashion_mnist

(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()

Si hacemos

X_train_full.shape

Nos devuelve  (60000, 28, 28) lo que significa que contiene 60.000 imágenes de 28 por 28 pixels.

Dividimos el dataset de entrenamiento completo en un dataset de validación y otro de entrenamiento (más pequeño). También escalamos las intensidades de píxeles para dejarlas dentro del rango 0-1, como sus valores van de 0 a 255 las dividimos entre 255, esto hace que pasen a ser valores flotantes.

X_valid, X_train = X_train_full[:5000] / 255, X_train_full[5000:] / 255

y_valid, y_train = y_train_full[:5000], y_train_full[5000:]

X_test = X_test / 255

Vamos a mostrar una imagen del conjunto

plt.imshow(X_train[23], cmap="binary")

plt.axis('off')

plt.show()

En este caso hemos tomado al azar el número 23 que ha resultado ser una bota.

class_names = ["Camiseta", "Pantalones", "Jersey", "Vestido", "Abrigo","Sandalia", "Camisa", "Deportivas", "Bolso", "Bota"]

Por ejemplo elegimos la etiqueta de nuestra imagen 23.

class_names[y_train[23]]

En nuestro caso está clasificada como deportivas.

El dataset de validación contiene 5000 imágenes y el dataset de prueba contiene 10000 imágenes:

X_valid.shape

X_test.shape

Crear un modelo usando la API Secuencial

Ahora vamos a construir una red neuronal  con dos capas ocultas

model = keras.models.Sequential()

model.add(keras.layers.Flatten(input_shape=[28, 28]))

model.add(keras.layers.Dense(300, activation="relu"))

model.add(keras.layers.Dense(100, activation="relu"))

model.add(keras.layers.Dense(10, activation="softmax"))

La primera fila crea el modelo secuencial, la segunda línea crea una capa de entrada aplanada (Flatten), su cometido es convertir cada imagen de 28x28 pixels en un array de una dimensión y 784 bits de tamaño, no tiene parámetros simplemente realiza un preprocesamiento.

La siguiente fila, crea una capa densa de 300 neuronas ( o perceptrones)  y utilizará la función ReLU como función de activación. Cada capa densa gestiona su propia matriz de pesos y contiene todas las conexiones con la capa de entrada, también gestiona los sesgos de cada neurona (Bias). 

La siguiente línea añade una segunda capa de 100 neuronas. Finalmente añadimos una capa de salida de 10 neuronas, una por clase. Y utiliza softmax como función de activación pues las 10 clases son exclusivas.

En vez de añadir las capas una por una, podemos pasar una lista de las capas al crear el modelo secuencial.

model = keras.models.Sequential([

    keras.layers.Flatten(input_shape=[28, 28]),

    keras.layers.Dense(300, activation="relu"),

    keras.layers.Dense(100, activation="relu"),

    keras.layers.Dense(10, activation="softmax")

])

Si queremos saber las capas que tiene nuestro modelo podemos hacer 

model.layers

También podemos ver un pequeño resumen de nuestra red poniendo

model.summary()

Y para ver un esquema 

keras.utils.plot_model(model, "mnist_modelo_prendas_ropa.png", show_shapes=True)

Para obtener el nombre de la primera capa oculta

hidden1 = model.layers[1]

hidden1.name

Esta devuelve true si la capa es oculta

model.get_layer(hidden1.name) is hidden1

Todos los parámetros de una capa pueden ser accedidos utilizando los métodos get_weights() y set_weghts() si la capa es densa, incluye los pesos de las conexiones y los términos de sesgo (bias).

weights, biases = hidden1.get_weights()

weights

weights.shape

biases

biases.shape

Compilando el modelo

Después de crear nuestro modelo necesitamos compilarlo, para ello llamamos al método compile 

model.compile(loss="sparse_categorical_crossentropy",

              optimizer="sgd",

              metrics=["accuracy"])

Para especificar la función de pérdida y el optimizador a utilizar. Opcionalmente podemos especificar una lista de métricas extra para computar durante el entrenamiento y evaluación.

hemos utilizado sparse_categorical_crossentropy porque tenemos etiquetas escasas (una por instancia) y las clases son exclusivas. Respecto al optimizador sgd significa que vamos a entrenar el modelo utilizando Descenso de gradiente estocástico simple (Stochastic Gradient Descent). Finalmente debido a que es un clasificador, es útil medir su exactitud "accuracy" durante su entrenamiento y evaluación.

Entrenando y evaluando el modelo

Ahora el modelo está preparado para ser entrenado, para ello llamamos al método fit().

history = model.fit(X_train, y_train, epochs=30,

                    validation_data=(X_valid, y_valid))

Para entrenar el modelo, le pasamos las características de entrada X_train y las clases objetivo y_train así como el número de épocas a entrenar, también le pasamos el set de validación aunque esto último es opcional. 

Keras mide la perdida y otras métricas del modelo al final de cada época, lo cual es muy útil para ver cómo se va entrenando el modelo.

Para ver los diferentes parámetros del entrenamiento

history.params

print(history.epoch)

history.history.keys()

Si creamos un diccionario con estos valores, podemos visualizar las gráficas del entrenamiento.

import pandas as pd

pd.DataFrame(history.history).plot(figsize=(8, 5))

plt.grid(True)

plt.gca().set_ylim(0, 1)

save_fig("curvas_de_aprendizaje_keras")

plt.show()

Una vez estamos satisfechos con la exactitud del modelo podemos evaluar el set para estimar el error antes de desplegarlo en producción. Podemos hacerlo fácilmente con el método evaluate().

model.evaluate(X_test, y_test)

313/313 [==============================] - 0s 2ms/step - loss: 0.3364 - accuracy: 0.8812

[0.33643999695777893, 0.8812000155448914]

Utilizando el modelo para hacer predicciones

A continuación utilizaremos el método predict() para hacer predicciones sobre nuevas instancias. Como no tenemos nuevas instancias reales, vamos a utilizar las cuatro primeras instancias del dataset

X_new = X_test[:4]

y_proba = model.predict(X_new)

y_proba.round(2)

array([[0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.01, 0.  , 0.99],

       [0.  , 0.  , 1.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ],

       [0.  , 1.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ],

       [0.  , 1.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  , 0.  ]],

      dtype=float32)

Para cada instancia estima una probabilidad por clase entre la 0 y la 9, para la primera instancia ha estimado una probabilidad de 0,99 a la clase 9 que es una bota, y 0,01 para la clase 7 que es deportivas. Lo mismo para el resto de instancias.

Si queremos obtener sólo un valor para la clase de mayor probabilidad, en vez del método predict() utilizaremos np.argmax().

y_pred =np.argmax(model.predict(X_new), axis=-1)

y_pred

array([9, 2, 1, 1])

para ver el significado de cada clase hacemos

np.array(class_names)[y_pred]

array(['Bota', 'Jersey', 'Pantalones', 'Pantalones'], dtype='<U10')

y para ver las imágenes

plt.figure(figsize=(7.2, 2.4))

for index, image in enumerate(X_new):

    plt.subplot(1, 4, index + 1)

    plt.imshow(image, cmap="binary", interpolation="nearest")

    plt.axis('off')

    plt.title(class_names[y_test[index]], fontsize=12)

plt.subplots_adjust(wspace=0.2, hspace=0.5)

save_fig('imagenes_predichas', tight_layout=False)

plt.show()

 

Clasificaciones Multiclase y Multietiqueta en Machine Learning

Anteriormente hemos visto la clasificación binaria donde clasificábamos entre dos tipos, es decir un objeto dado es un objeto de nuestra clasificación, o no lo es. Y tomábamos como ejemplo el 7, un número dado es un 7 o no lo es. Pues bien en la clasificación multiclase, dado un numero tenemos que clasificarlo dentro de las clases posibles, es decir, o es un 0, o un 1, o un 2, etc.

Hay algoritmos estrictamente binarios, como la Regresión Logística, o los clasificadores SVM (Support Vector Machine), otros algoritmos como los SGD, los Random Forest y los naive Bayes son multiclasificadores. Aunque también se pueden utilizar clasificadores binarios para multiclasificación, por ejemplo podemos entrenar 10 modelos SVM, uno para clasificar los ceros, otro para los unos, otro para los doses, etc, y dada una instancia clasificarla con la que mayor puntuación obtenga en los 10 clasificadores, esto se llama estrategia OvR (One versus de rest).

Otra estrategia podría ser entrenar los modelos para distinguir entre 0 y 1, otro modelo entre 0 y 2, otro entre 1 y 2, etc esta estrategia se llama OvO (One versus one). Para esta estrategia, si tenemos N clases necesitamos N x (N-1)/2 modelos, en el caso de 0 a 9 tenemos ¡45 modelos a entrenar! Aunque tiene la ventaja de que cada modelo sólo necesita un subset para entrenarse.

SVM tiene un desempeño pobre con datasets muy grandes, en este caso es mejor utilizar OvO pues es más rápido entrenando cada trozo de subset.

Si no hemos hecho el post anterior, para que funcione el código siguiente, es necesario ejecutar antes este código:

# Python ≥3.5 is required

import sys

assert sys.version_info >= (3, 5)

 

# Scikit-Learn ≥0.20 is required

import sklearn

assert sklearn.__version__ >= "0.20"

 

# Common imports

import numpy as np

import os

 

# to make this notebook's output stable across runs

np.random.seed(42)

 

# To plot pretty figures

%matplotlib inline

import matplotlib as mpl

import matplotlib.pyplot as plt

mpl.rc('axes', labelsize=14)

mpl.rc('xtick', labelsize=12)

mpl.rc('ytick', labelsize=12)

 

#importar tensorflow y el script input_data

import tensorflow as tf

import input_data

 

#importamos el dataset mnist

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', version=1)

mnist.keys()

 

#importamos matplotlib para generar graficos

%matplotlib inline

import matplotlib as mpl

import matplotlib.pyplot as plt

some_digit = X[0]

 

#definimos X e y

X, y = mnist["data"], mnist["target"]

 

from sklearn.svm import SVC

svm_clf = SVC(gamma="auto", random_state=42)

svm_clf.fit(X_train[:1000], y_train[:1000]) # y_train

svm_clf.predict([some_digit])

En Scikit-Learn podemos lanzar un algoritmo OvO utilizando OneVsOneClassifier y OvR con OneVrRestClassifier basta con crear una instancia y pasar un clasificador como constructor. Por ejemplo el siguiente código crea un clasificador multiclase basado en SVC usando OvR.

from sklearn.multiclass import OneVsRestClassifier

ovr_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))

ovr_clf.fit(X_train[:1000], y_train[:1000])

ovr_clf.predict([some_digit])

Devuelve 0 pues en el post anterior definimos un cero del dataset con some_digit = X[234]

len(ovr_clf.estimators_)

Devuelve 

10

Entrenar un SGDClassifier es aún más fácil

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)

sgd_clf.fit(X_train, y_train)

sgd_clf.predict([some_digit])

Esta vez Sckit-Learn no ha corrido OvR ni OvO porque SGD soporta clasificación multiclase el método decision_function() devuelve un valor para cada clase, vamos a ver las puntuaciones obtenidas

sgd_clf.decision_function([some_digit])

Devuelve

array([[  3816.04556036, -32544.8070744 ,  -8613.62680163,

         -4792.16972022, -10146.9498229 ,  -4250.27483221,

        -21170.5186733 , -22260.53591175,  -2863.12785007,

        -16907.17784199]])

Podemos ver que el clasificador está bastante acertado con su predicción, pues todas las puntuaciones son negativas, mientras que la del 0 es positiva. 

Ahora queremos evaluar este clasificador, para ellos utilizamos validación cruzada como siempre. Utilizaremos la función cross_val_score() para utilizar la exactitud del clasificador  SGDClassifier

from sklearn.model_selection import cross_val_score

cross_val_score(sgd_clf,X_train,y_train,cv=3,scoring="accuracy")

Devuelve

array([0.87365, 0.85835, 0.8689 ])

Esto es un 85% como mínimo en todos los testeos, si hubiésemos utilizado un clasificador aleatorio obtendríamos un 10%, no está mal, pero podemos mejorarlo simplemente escalando las entradas 

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))

cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")

Análisis de error

Primero echaremos un vistazo a la matriz de confusión, necesitamos hacer predicciones utilizando la función cross_val_predict() y luego llamando a la función matriz de confusión confusión_matrix() Las filas muestran los números etiquetados (reales) y las columnas los números predichos,

y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)

conf_mx = confusion_matrix(y_train, y_train_pred)

conf_mx

Devuelve

array([[5577,    0,   22,    5,    8,   43,   36,    6,  225,    1],

       [   0, 6400,   37,   24,    4,   44,    4,    7,  212,   10],

       [  27,   27, 5220,   92,   73,   27,   67,   36,  378,   11],

       [  22,   17,  117, 5227,    2,  203,   27,   40,  403,   73],

       [  12,   14,   41,    9, 5182,   12,   34,   27,  347,  164],

       [  27,   15,   30,  168,   53, 4444,   75,   14,  535,   60],

       [  30,   15,   42,    3,   44,   97, 5552,    3,  131,    1],

       [  21,   10,   51,   30,   49,   12,    3, 5684,  195,  210],

       [  17,   63,   48,   86,    3,  126,   25,   10, 5429,   44],

       [  25,   18,   30,   64,  118,   36,    1,  179,  371, 5107]])

Hay un montón de números, si queremos una representación gráfica podemos hacer 

plt.matshow(conf_mx, cmap=plt.cm.gray)

plt.show()

Esta representación de la matriz de confusión es bastante mejor, pues vemos que las imágenes pertenecientes a la diagonal se han clasificado correctamente, es decir la mayoría de ceros se ha clasificado como cero, los unos como uno, etc. Podemos ver que el 5 es un poco más oscuro que el resto, lo que significa que hay unas pocas imágenes de 5 que se han clasificado erróneamente.

Vamos a eliminar la diagonal para centrarnos en los errores

row_sums = conf_mx.sum(axis=1, keepdims=True)

norm_conf_mx = conf_mx / row_sums

np.fill_diagonal(norm_conf_mx, 0)

plt.matshow(norm_conf_mx, cmap=plt.cm.gray)

save_fig("confusion_matrix_errors_plot", tight_layout=False)

plt.show()

 

Podemos ver claramente los diferentes tipos de errores que ha cometido el clasificador. Recuerda que las filas representan los números reales, mientras que las columnas representas los números predichos. La columna del 8 es bastante clara, lo que indica que muchos números han sido clasificados de forma errónea como ocho, sin embargo la fila 8 es bastante oscura, lo que indica que la mayoría de los ochos se han clasificado correctamente como 8.

Esta matriz de confusión no tiene porqué ser simétrica, también podemos ver que se clasifican muchos 5 como 3 y muchos 3 como 5.

Echando un vistazo a esta matriz podemos ver que nuestros esfuerzos se deben centrar en reducir los falsos ochos y tratar de solucionar los intercambios entre 3 y 5. Centrémonos en este último punto. Por ejemplo vamos a mostrar los 3 y 5 que se han clasificado mal,

cl_a, cl_b = 3, 5

X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]

X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]

X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]

X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]

 

plt.figure(figsize=(8,8))

plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)

plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)

plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)

plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)

save_fig("analisis de erorres de 3 y 5")

plt.show()

Los dos bloques de la izquierda muestran dígitos clasificados como 3 y los dos bloques de la derecha los clasificados como 5. Algunos dígitos se han clasificado erróneamente (arriba-derecha y abajo izquierda)

Clasificación Multietiqueta (Multilabel)

Hasta ahora hemos asignado cada instancia a una sola clase, pero puede ser que deseemos clasificar en múltiples clases cada instancia. Por ejemplo si deseamos clasificar diferentes personas en diferentes fotos el clasificador deberá ser entrenado para reconocer digamos a Pepe, María y Luis y de este modo si en una foto sale María y Pepe el clasificador devolverá [1,1,0] significa que en dicha foto salen Pepe y María pero no Luis. Tal sistema de clasificación se llama clasificación multietiqueta.

El siguiente código genera un array multietiqueta que contiene dos etiquetas por cada dígito. La primera etiqueta indica si el número es grande o no (7,8 o 9) y el segundo indica si es o no impar.

from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)

y_train_odd = (y_train % 2 == 1)

y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()

knn_clf.fit(X_train, y_multilabel)

Las siguientes líneas crean una instancia KNeighborsClassifier  que devuelve dos etiquetas.

knn_clf.predict([some_digit])

Este es el resultado

array([[False, False]])

Una aproximación es medir la puntuación F1 para cada etiqueta individual, el código a continuación calcula la puntuación media F1

ojo la ejecución de esta línea puede tardar horas

y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)

f1_score(y_multilabel, y_train_knn_pred, average="macro")

0.976410265560605

Clasificación Multioutput

Es una generalización de la clasificación multilabel, para ilustrarlo vamos a construir un sistema que quita el ruido de las imágenes

noise = np.random.randint(0, 100, (len(X_train), 784))

X_train_mod = X_train + noise

noise = np.random.randint(0, 100, (len(X_test), 784))

X_test_mod = X_test + noise

y_train_mod = X_train

y_test_mod = X_test

some_index = 0

plt.subplot(121); plot_digit(X_test_mod[some_index])

plt.subplot(122); plot_digit(y_test_mod[some_index])

save_fig("ejemplo_de_ruido")

plt.show()

A la izquierda se muestra la imagen con ruido y a la derecha sin ruido

 

Finalmente entrenaremos el clasificador para limpiar aún más esta imagen.

knn_clf.fit(X_train_mod, y_train_mod)

clean_digit = knn_clf.predict([X_test_mod[some_index]])

plot_digit(clean_digit)

save_fig("digito_limpio")

Vemos que finalmente queda bastante cercana al objetivo.