Clasificadores binarios en Machine Learning

Vamos a tratar algoritmos de clasificación, y además vamos a hacerlo con un dataset de imágenes. En este caso vamos a utilizar números manuscritos y vamos a tratar de clasificar cada número dentro de su categoría. Es decir clasificaremos los unos manuscritos como 1, los doses como 2, etc. De modo que podamos leer números manuscritos de una foto e interpretarlos como números.

Lo primero que vamos a hacer es descargar las librerías adecuadas para tratar nuestro dataset, para ello hacemos

Fotos como esta

 

# Es necesaria una versión superior a Python 3.5

import sys

assert sys.version_info >= (3, 5)

 

# Es necesaria una versión de Scikit-Learn superior a ≥0.20

import sklearn

assert sklearn.__version__ >= "0.20"

 

# importaciones communes

import numpy as np

import os

 

# para hacer que la salida de este código sea estable en todas las ejecuciones

np.random.seed(42)

 

# para que muestre imágenes amigables

%matplotlib inline

import matplotlib as mpl

import matplotlib.pyplot as plt

mpl.rc('axes', labelsize=14)

mpl.rc('xtick', labelsize=12)

mpl.rc('ytick', labelsize=12)

 

# Las imágenes se guardarán en C:\Usuarios\Usuario_Principal\imagenes\clasificacion (C:\Usuarios\Usuario_principal es la ruta de la instalación original de anaconda)

#C:\ Usuarios\Usuario_Principal es también la ruta por defecto de los notebook de Jupyter

 

PROJECT_ROOT_DIR = "."

CHAPTER_ID = "clasificacion"

IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "imagenes", CHAPTER_ID)

os.makedirs(IMAGES_PATH, exist_ok=True)

 

def save_fig(fig_id, tight_layout=True, fig_extension="jpg", resolution=300):

    path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)

    print("Imagen Guardada", fig_id)

    if tight_layout:

        plt.tight_layout()

    plt.savefig(path, format=fig_extension, dpi=resolution)

Descargamos el Dataset MNIST de caracteres numéricos manuscritos

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', version=1)

mnist.keys()

El data set se descarga en

C:\Users\Usuario\scikit_learn_data\openml\openml.org\data\v1\download

Y no tiene extensión, es un buen ejercicio descomprimir el dataset y abrirlo con notepad++ para ver su estructura interna. Para usuarios avanzados dejo la tarea de convertir una imagen real de varios carácteres en un subdataset con la misma estructura que este y leerlo con la red entrenada.

Los datasets cargados por Scikit-Learn generalmente tienen una estructura de diccionario similar, incluyendo lo siguiente:

DESCR es la clave que describe el dataset

Una palabra clave “data” contiene un array con una fila por instancia y una columna por característica

La palabra clave “target” contiene un array con las etiquetas

Vamos a echar un vistazo a estos arrays

X, y = mnist["data"], mnist["target"]

X.shape

Nos devuelve (70000, 784)

y.shape

Nos devuelve (70000,)

Hay 70000 imágenes y cada una tiene 784 características. Esto es debido a que cada imagen tiene 28 x 28 pixels. Cada característica representa la intensidad de cada pixel entre 0 (blanco) y 255 (negro)

Vamos a mostrar un dígito del dataset, para ello debemos extraer un vector de características del dataset,  reubicarlo en una matriz de 28x28 y mostrarlo. En este caso hemos tomado al azar el array Nº 234.

%matplotlib inline

import matplotlib as mpl

import matplotlib.pyplot as plt

some_digit = X[234]

some_digit_image = some_digit.reshape(28, 28)

plt.imshow(some_digit_image, cmap=mpl.cm.binary)

plt.axis("off")

save_fig("some_digit_plot")

plt.show()

 

 

Para ver la etiqueta que le han asignado hacemos

y[234]

(en nuestro caso 234 es el número que hemos elegido al azar)

Nos devuelve la cadena “0”. La mayoría de los algoritmos de ML esperan números, así que lo convertimos a número con;

y = y.astype(np.uint8)

Para entrenar nuestros algoritmos podemos utilizar 60000 imágenes y dejar 10000 para testearlo. Esto sirve en este caso que el dataset está barajado aleatoriamente, si estuviera ordenado no serviría.

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

Clasificadores binarios

Para simplificar el problema vamos a clasificar sólo un dígito, vamos a hacer un clasificador binario entre el número 7 y todo lo que no sea número 7.

y_train_7 = (y_train == 7)

y_test_7 = (y_test == 7)

Ahora elegimos un clasificador binario y lo entrenamos. Para empezar comenzaremos con un clasificador de descenso de gradiente estocástico, utilizaremos SGDClassifier de Scikit-Learn, este clasificador tiene la ventaja de ser capaz de tratar datasets muy grandes de forma eficiente.

Crearemos el clasificador y lo entrenaremos con el dataset completo.

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)

sgd_clf.fit(X_train, y_train_7)

El clasificador es aleatorio (el parámetro random_state introduce la semilla aleatoria) en este caso hemos puesto 42 de ahí el nombre de Estocástico.

Ahora lo podemos utilizar para detectar imágenes del número 7.

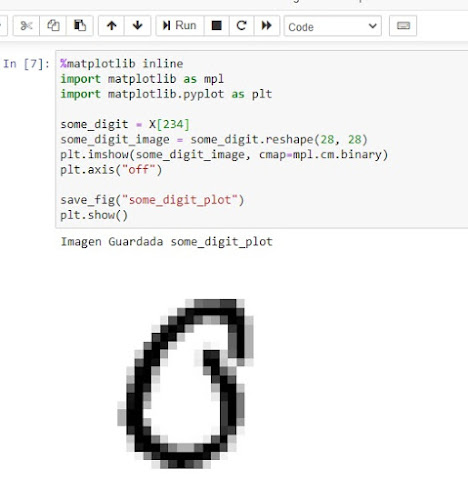
sgd_clf.predict([some_digit])

En nuestro caso devuelve false, pues hemos cargado some_digit = X[234]  que corresponde con el cero.

Evaluando el modelo con Cross-Validation

Vamos a utilizar la función  cross_val_score() para evaluar nuestro modelo de  SDGClassifier. Vamos a partir el dataset en tres subsets para hacer predicciones y evaluar el modelo

from sklearn.model_selection import cross_val_score

cross_val_score(sgd_clf, X_train, y_train_7, cv=3, scoring="accuracy")

array([0.98105, 0.9735 , 0.95335])

Hemos obtenido unos valores bastante buenos, pero es un clasificador muy tonto que sólo tiene en cuenta si es un 7 o no.

from sklearn.base import BaseEstimator

class Never7Classifier(BaseEstimator):

    def fit(self, X, y=None):

        pass

    def predict(self, X):

        return np.zeros((len(X), 1), dtype=bool)

y evaluamos la precisión del modelo así

never_7_clf = Never7Classifier()

cross_val_score(never_7_clf, X_train, y_train_7, cv=3, scoring="accuracy")

En nuestro caso sale una precisión del 89%, esto es debido a que sólo el 10% de las imágenes son 7´s y el 90% restante son otros números, lo cual demuestra que la precisión no es la medida de ejecución preferida para los clasificadores, especialmente con datasets sesgados como en este caso (cuando algunas clases son mucho más frecuentes que otras)

Matriz de confusión

Una vía mejor para evaluar la ejecución de un clasificador, es la matriz de confusión. La idea general consiste en  contar el número de instancias de clase A que son clasificadas como clase B. Por ejemplo para saber el número de veces que se clasifica una imagen de 7 como si fuera un 1 tendríamos que mirar en la séptima fila y la primera columna de la matriz de confusión.

Necesitamos un set de predicciones comparado con sus valores reales, pero no queremos tocar nuestro dataset pues lo vamos a necesitar intacto hasta el final (cuando lancemos nuestra aplicación) así que vamos a utilizar la función 

cross_val_predict()

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train,y_train_7, cv=3)

Las predicciones que hace esta función son claras, significando claras que la predicción que realiza el modelo nunca ha visto los datos durante el entrenamiento. Ahora creamos la matriz de confusión pasando la clase objetico (y_train_7) y la clase de valores predichos (y_train_pred)

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_7, y_train_pred)

array([[52581,  1154],

       [  688,  5577]], dtype=int64)

Cada fila de la matriz de confusión  representa una clase real, mientras que cada columna representa una clase predicha. La primera fila de nuestra matriz particular considera todas las imágenes que no son 7´s (52.581) las que fueron correctamente clasificadas como que no son 7´s (las llamadas negativos verdaderos) mientras que las restantes 1.154 son las imágenes que se clasificaron incorrectamente como 7´s. (positivos falsos La segunda fila considera las imágenes de 7´s (la clase positiva) 688 fueron incorrectamente clasificadas como 7 sin serlo (negativos falsos)  mientras que las restantes 5.577 fueron correctamente clasificadas como 7 (positivos verdaderos).

Nota. Hay que tener en cuenta que esta parte de Machine Learning se llama supervisada, pues los datasets además de la imagen, traen una etiqueta asociada e  introducida manualmente por un humano, que indica el valor real de la imagen.

Un clasificador perfecto debería devolver sólo positivos verdaderos y negativos verdaderos. De modo que la matriz de confusión debería tener valores sólo en su diagonal principal.

y_train_perfect_predictions = y_train_7  # pretendemos alcanzar la perfección, para ello utilizamos las etiquetas (valores y)

confusion_matrix(y_train_7, y_train_perfect_predictions)

array([[53735,     0],

       [    0,  6265]], dtype=int64)

Precisión y Recuerdo 

Scikit-Learn tiene varias funciones para calcular las métricas de clasificación, entre ellas precisión y recuerdo.

from sklearn.metrics import precision_score, recall_score

precision_score(y_train_7, y_train_pred)

0.8285544495617293

Es igual que 

5577 / (5577 + 1154)

Este valor indica que el 82,85 % de las veces clasifica correctamente un 7 (Precisión)

recall_score(y_train_5, y_train_pred)

0.8901835594573024

Es igual que 

5577 / (5577 + 688)

Este valor indica que detecta el 89,01 % de los 7´s (Recuerdo)

Es conveniente combinar precisión y recuero en una métrica sencilla llamada F1

Lo calculamos del siguiente modo

from sklearn.metrics import f1_score

f1_score(y_train_7, y_train_pred)

0.7420962043663375

Que es igual que 

5577 / (5577 + (1154 + 688) / 2)

En función de si deseamos tener falsos positivos o no podemos permitirnoslo, deberemos primar la precisión o el recuerdo. Lamentablemente si incrementamos la precisión reducimos el recuerdo y viceversa. Esto se llama renuncia precisión/recuerdo.

Compensación precisión/recuerdo (Precision/Recall trade-off)

Como la precisión y el recuerdo son dos características opuestas, su compensación no es más que tomar la decisión de que peso dar a estas características, por ejemplo 50% de precisión y 50% de recuerdo, o 20%-80% o 40%-60% dependiendo del problema concreto que estemos abordando y el resultado que deseemos obtener.

En el caso que nos ocupa podemos desear que ningún 7 pase por alto, con lo que aumentaremos el recuerdo y disminuiremos la precisión, de modo que sabemos que detectaremos el 100% de los 7 aun siendo conscientes de que se nos pueden colar caracteres que no sean 7.  Mientras que si queremos estar seguros de que el 100% de los 7´s detectados sean 7 y no otro carácter, entonces disminuiremos el recuerdo y aumentaremos la precisión.

Scikit-Learn no nos permite elegir el umbral directamente, pero nos permite acceder a las puntuaciones de decisión que utiliza para hacer predicciones. Podemos llamar al método decision_function() que devuelve una puntuación para cada instancia y utilizarlo como umbral para hacer predicciones basándonos en sus puntuaciones.

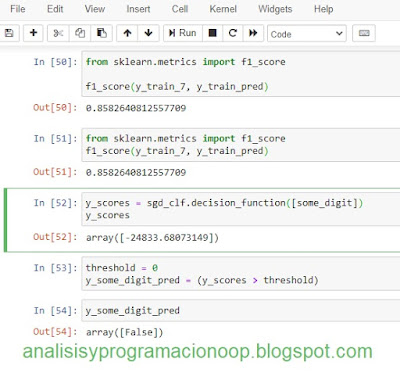
y_scores = sgd_clf.decision_function([some_digit])

y_scores

threshold = 0

y_some_digit_pred = (y_scores > threshold)

y_some_digit_pred

SGDCClassifier utiliza un umbral igual a 0 así que el código anterior devuelve el mismo resultado que el método predict()

sgd_clf.predict([some_digit])

Vamos a borrar el umbral

threshold = 8000

y_some_digit_pred = (y_scores > threshold)

y_some_digit_pred

¿como decidimos que umbral conviene utilizar? Primero utilizamos la función cross_val_predict() para obtener las puntuaciones de todas las instancias del set de entrenamiento pero esta vez vamos a especificar que queremos que devuelva las puntuaciones de decisión en vez de las de predicción.

y_scores = cross_val_predict(sgd_clf, X_train, y_train_7, cv=3,method="decision_function")

Con estas puntuaciones utilizamos la función precisión_recall_curve() para ver todos los posibles umbrales.

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_7, y_scores)

Finalmente utilizamos Matplotlib para mostrar nuestras funciones de precisión y recuerdo y sus umbrales.

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):

    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)

    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)

    plt.legend(loc="center right", fontsize=16)

    plt.xlabel("Threshold", fontsize=16)       

    plt.grid(True)                            

    plt.axis([-50000, 50000, 0, 1])            

recall_90_precision = recalls[np.argmax(precisions >= 0.90)]

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]

plt.figure(figsize=(8, 4))                                                                 

plot_precision_recall_vs_threshold(precisions, recalls, thresholds)

plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")                

plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")                               

plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")

plt.plot([threshold_90_precision], [0.9], "ro")                                           

plt.plot([threshold_90_precision], [recall_90_precision], "ro")                           

save_fig("precision_recall_vs_threshold_plot")                                             

plt.show()

 

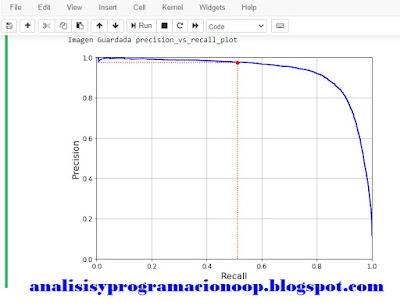
Otra vía para elegir una buena compensación de precisión y recuerdo es dibujar la gráfica de la precisión directamente contra la de recuerdo.

(y_train_pred == (y_scores > 0)).all()

def plot_precision_vs_recall(precisions, recalls):

    plt.plot(recalls, precisions, "b-", linewidth=2)

    plt.xlabel("Recuerdo", fontsize=16)

    plt.ylabel("Precision", fontsize=16)

    plt.axis([0, 1, 0, 1])

    plt.grid(True)

 

plt.figure(figsize=(8, 6))

plot_precision_vs_recall(precisions, recalls)

plt.plot([0.5123, 0.5123], [0., 0.975], "r:")

plt.plot([0.0, 0.5123], [0.975, 0.975], "r:")

plt.plot([0.5123], [0.975], "ro")

save_fig("precision_vs_recall_plot")

plt.show()

 

Aquí podemos ver que la precisión comienza a caer abruptamente hacia el 80% del recuerdo. Si queremos seleccionar un valor precisión/recuerdo justo antes de dicha caída, elegiríamos por ejemplo en torno al 60 %  de recuerdo, pero esto siempre dependerá de lo que deseemos en nuestro proyecto.

Supongamos que queremos una precisión del 90%. En la primera gráfica vemos que esto se produce en torno al valor umbral 2000. Si queremos ser más precisos podemos seleccionar el umbral más bajo que nos dé al menos un 90% de precisión np.argmax() nos dará el primer índice del valor máximo, en este caso significa el primer valor que devuelva true.

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]

threshold_90_precision

Nos devuelve 2288

Vamos a ver los valores de precisión y recuerdo

y_train_pred_90 = (y_scores >= threshold_90_precision)

precision_score(y_train_7, y_train_pred_90)

0.9000864304235091

recall_score(y_train_7, y_train_pred_90)

0.8311252992817239

Ya  tenemos los datos para ajustar nuestro clasificador al 90% de precisión. De este modo es sencillo crear un clasificador con los valores de precisión que deseemos. Pero ojo, porque un  clasificador de muy alta precisión no es muy útil si el recuerdo es muy bajo.

Característica Operativa del Receptor (Receiver Operating Characteristic ROC)

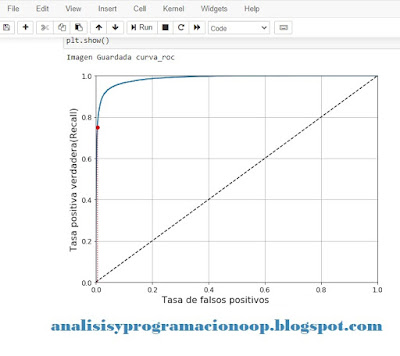
La característica operativa del receptor es una herramienta común utilizada para clasificadores binarios. Es muy similar a la técnica precisión/recuerdo pero en vez de mostrar la precisión en función del recuerdo, muestra la tasa de positivos verdaderos (otro nombre para recuerdo [recall]) contra la tasa de falsos positivos (FPR), es decir los que se consideran dentro de una clase sin serlo. La tasa negativa verdadera (true negative rate TNR) son los valores se han clasificado correctamente como no pertenecientes a una clase, también ee llamada especifidad (specifity). Por tanto ROC muestra la relación entre la sensitividad (recuerdo) y la especificidad. Para ello utilizaremos la función roc_curve() para varios umbrales diferentes.

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_7, y_scores)

def muestra_curva_roc(fpr, tpr, label=None):

    plt.plot(fpr, tpr, linewidth=2, label=label)

    plt.plot([0, 1], [0, 1], 'k--') # diagonal de puntos

    plt.axis([0, 1, 0, 1])                                   

    plt.xlabel('Tasa de falsos positivos', fontsize=16)

    plt.ylabel('Tasa positiva verdadera (Recall)', fontsize=16)   

    plt.grid(True)                                          

plt.figure(figsize=(8, 6))                        

plot_roc_curve(fpr, tpr)

plt.plot([5.837e-3, 5.837e-3], [0., 0.75], "r:")

plt.plot([0.0, 5.837e-3], [0.75, 0.75], "r:") 

plt.plot([5.837e-3], [0.75], "ro")              

save_fig("curva_roc")                        

plt.show()

Una vez más tenemos una relación de compensación, esta vez entre el  recuerdo (TCR) y los falsos positivos (FPR) la línea de puntos representa la curva ROC que sería un clasificador puramente aleatorio, de modo que un buen clasificador se alejaría de esta línea de puntos y se acercará a la esquina superior izquierda. El punto rojo representa el valor elegido del 75% de recuerdo.

Una forma de comparar clasificadores es medir el área que hay bajo la curva, un clasificador perfecto tendría un área unidad mientras que uno aleatorio tendrá un área de 0,5. Scikit-Learn tiene una forma de medir esa área con 

from sklearn.metrics import roc_auc_score

roc_auc_score(y_train_7, y_scores)

Esto nos devuelve

0.986670497551944

Como la curva ROC es bastante similar a la de Precisión/Recuerdo, nos preguntaremos cual de las dos utilizar, para decidirnos conviene utilizar la regla del pulgar. Esta dice que preferiremos la curva Precisión/Recuerdo cuando la clase de positivos sea rara o cuando deseemos tener más cuidado con los falsos positivos que con los falsos negativos. En otro caso elegiremos la curva ROC.

Ahora vamos  a entrenar un RandomForestClassifier y vamos a comparar su curva ROC y el valor del área de la curva con las correspondientes de SGDClassifier.

from sklearn.ensemble import RandomForestClassifier

forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)

y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_7, cv=3, method="predict_proba")

La función roc_curve espera etiquetas y puintuaciones, pero en lugar de puntuaciones tenemos las probabilidades de cada clase, así que utilizaremos la probabilidad positiva de la clase como puntuación.

y_scores_forest = y_probas_forest[:, 1] # puntuación  = proba de clase positiva

fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_7,y_scores_forest)

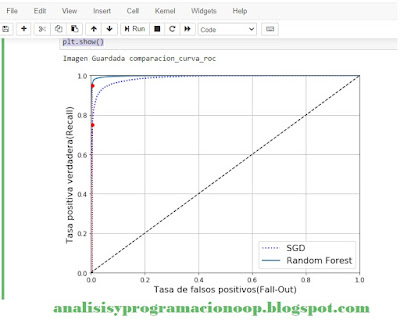
Ahora ya está listo para mostrar la curva ROC

plt.figure(figsize=(8, 6))

plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")

plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")

plt.plot([5.837e-3, 5.837e-3], [0., 0.75], "r:")

plt.plot([0.0, 5.837e-3], [0.75, 0.75], "r:")

plt.plot([5.837e-3], [0.75], "ro")

plt.plot([5.837e-3,5.837e-3], [0., 0.9487], "r:")

plt.plot([5.837e-3], [0.9487], "ro")

plt.grid(True)

plt.legend(loc="lower right", fontsize=16)

save_fig("comparacion_curva_roc")

plt.show()

  

Como podemos ver en la imagen la curva de RandomForest  es mucho mejor que la de SGDCClassifier, pues está más pegada a la esquina superior izquierda y su área es más cercana a 1.

roc_auc_score(y_train_7, y_scores_forest)

0.9982747530426836

y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_7, cv=3)

precision_score(y_train_7, y_train_pred_forest)

0.986736474694589

recall_score(y_train_7, y_train_pred_forest)

0.9024740622505986

Con lo que tenemos un 98,67 % de precisión y un 90,24 % de recuerdo, no está mal.