Ya hemos comentado aquí lo que es una red neuronal, ahora vamos a descargar el dataset MNIST de prendas de ropa que contiene 60.000 imágenes de prendas de vestir en escala de grises de 28x28 pixels. El dataset contiene 10 categorías o clases de prendas de vestir. Previamente tendremos instalado en nuestro equipo un entorno virtual de Anaconda con Tensorflow instalado (enlace), o podemos optar también por ejecutar las instrucciones en la nube con Colaboratory.
Hecho esto importamos Tensorflow y Keras
import tensorflow as tf
from tensorflow import keras
Cargamos el dataset de Moda de MNIST
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()
Si hacemos
X_train_full.shape
Nos devuelve (60000, 28, 28) lo que significa que contiene 60.000 imágenes de 28 por 28 pixels.
Dividimos el dataset de entrenamiento completo en un dataset de validación y otro de entrenamiento (más pequeño). También escalamos las intensidades de píxeles para dejarlas dentro del rango 0-1, como sus valores van de 0 a 255 las dividimos entre 255, esto hace que pasen a ser valores flotantes.
X_valid, X_train = X_train_full[:5000] / 255, X_train_full[5000:] / 255
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255
Vamos a mostrar una imagen del conjunto
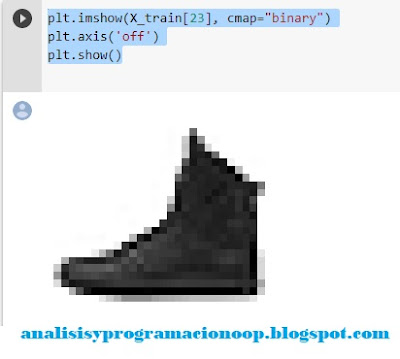
plt.imshow(X_train[23], cmap="binary")
plt.axis('off')
plt.show()
En este caso hemos tomado al azar el número 23 que ha resultado ser una bota.
class_names = ["Camiseta", "Pantalones", "Jersey", "Vestido", "Abrigo","Sandalia", "Camisa", "Deportivas", "Bolso", "Bota"]
Por ejemplo elegimos la etiqueta de nuestra imagen 23.
class_names[y_train[23]]
En nuestro caso está clasificada como deportivas.
El dataset de validación contiene 5000 imágenes y el dataset de prueba contiene 10000 imágenes:
X_valid.shape
X_test.shape
Crear un modelo usando la API Secuencial
Ahora vamos a construir una red neuronal con dos capas ocultas
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
La primera fila crea el modelo secuencial, la segunda línea crea una capa de entrada aplanada (Flatten), su cometido es convertir cada imagen de 28x28 pixels en un array de una dimensión y 784 bits de tamaño, no tiene parámetros simplemente realiza un preprocesamiento.
La siguiente fila, crea una capa densa de 300 neuronas ( o perceptrones) y utilizará la función ReLU como función de activación. Cada capa densa gestiona su propia matriz de pesos y contiene todas las conexiones con la capa de entrada, también gestiona los sesgos de cada neurona (Bias).
La siguiente línea añade una segunda capa de 100 neuronas. Finalmente añadimos una capa de salida de 10 neuronas, una por clase. Y utiliza softmax como función de activación pues las 10 clases son exclusivas.
En vez de añadir las capas una por una, podemos pasar una lista de las capas al crear el modelo secuencial.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
Si queremos saber las capas que tiene nuestro modelo podemos hacer
model.layers
También podemos ver un pequeño resumen de nuestra red poniendo
model.summary()
Y para ver un esquema
keras.utils.plot_model(model, "mnist_modelo_prendas_ropa.png", show_shapes=True)
Para obtener el nombre de la primera capa oculta
hidden1 = model.layers[1]
hidden1.name
Esta devuelve true si la capa es oculta
model.get_layer(hidden1.name) is hidden1
Todos los parámetros de una capa pueden ser accedidos utilizando los métodos get_weights() y set_weghts() si la capa es densa, incluye los pesos de las conexiones y los términos de sesgo (bias).
weights, biases = hidden1.get_weights()
weights
weights.shape
biases
biases.shape
Compilando el modelo
Después de crear nuestro modelo necesitamos compilarlo, para ello llamamos al método compile
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
Para especificar la función de pérdida y el optimizador a utilizar. Opcionalmente podemos especificar una lista de métricas extra para computar durante el entrenamiento y evaluación.
hemos utilizado sparse_categorical_crossentropy porque tenemos etiquetas escasas (una por instancia) y las clases son exclusivas. Respecto al optimizador sgd significa que vamos a entrenar el modelo utilizando Descenso de gradiente estocástico simple (Stochastic Gradient Descent). Finalmente debido a que es un clasificador, es útil medir su exactitud "accuracy" durante su entrenamiento y evaluación.
Entrenando y evaluando el modelo
Ahora el modelo está preparado para ser entrenado, para ello llamamos al método fit().
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid))
Para entrenar el modelo, le pasamos las características de entrada X_train y las clases objetivo y_train así como el número de épocas a entrenar, también le pasamos el set de validación aunque esto último es opcional.
Keras mide la perdida y otras métricas del modelo al final de cada época, lo cual es muy útil para ver cómo se va entrenando el modelo.
Para ver los diferentes parámetros del entrenamiento
history.params
print(history.epoch)
history.history.keys()
Si creamos un diccionario con estos valores, podemos visualizar las gráficas del entrenamiento.
import pandas as pd
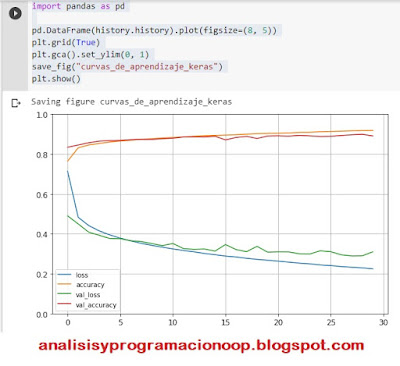
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("curvas_de_aprendizaje_keras")
plt.show()
Una vez estamos satisfechos con la exactitud del modelo podemos evaluar el set para estimar el error antes de desplegarlo en producción. Podemos hacerlo fácilmente con el método evaluate().
model.evaluate(X_test, y_test)
313/313 [==============================] - 0s 2ms/step
- loss: 0.3364 - accuracy: 0.8812
[0.33643999695777893, 0.8812000155448914]
Utilizando el modelo para hacer predicciones
A continuación utilizaremos el método predict() para hacer predicciones sobre nuevas instancias. Como no tenemos nuevas instancias reales, vamos a utilizar las cuatro primeras instancias del dataset
X_new = X_test[:4]
y_proba = model.predict(X_new)
y_proba.round(2)
array([[0. , 0. ,
0. , 0.
, 0. , 0. , 0. ,
0.01, 0. , 0.99],
[0.
, 0. , 1. , 0. ,
0. , 0.
, 0. , 0. , 0. ,
0. ],
[0.
, 1. , 0. , 0. ,
0. , 0.
, 0. , 0. , 0. ,
0. ],
[0.
, 1. , 0. , 0. ,
0. , 0.
, 0. , 0. , 0. ,
0. ]],
dtype=float32)
Para cada instancia estima una probabilidad por clase entre la 0 y la 9, para la primera instancia ha estimado una probabilidad de 0,99 a la clase 9 que es una bota, y 0,01 para la clase 7 que es deportivas. Lo mismo para el resto de instancias.
Si queremos obtener sólo un valor para la clase de mayor probabilidad, en vez del método predict() utilizaremos np.argmax().
y_pred =np.argmax(model.predict(X_new), axis=-1)
y_pred
array([9, 2, 1, 1])
para ver el significado de cada clase hacemos
np.array(class_names)[y_pred]
array(['Bota', 'Jersey', 'Pantalones', 'Pantalones'], dtype='<U10')
y para ver las imágenes
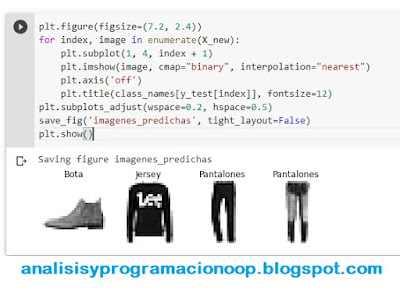
plt.figure(figsize=(7.2, 2.4))
for index, image in enumerate(X_new):
plt.subplot(1, 4, index + 1)
plt.imshow(image, cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_test[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('imagenes_predichas', tight_layout=False)
plt.show()




Muy bueno! muchas gracias
ResponderEliminar