Vamos a ver cómo seleccionar y ajustar hiperparámetros para redes neuronales densas usando hiperparámetros.
Antes de comenzar a usar hyperas, debemos comprender la biblioteca de Python llamada hyperopt. Hyperopt proporciona la capacidad de optimizar los espacios de búsqueda de dimensiones reales, valoradas, discretas y condicionales. Hyperas, es un envoltorio alrededor de hyperopt para una creación de prototipos más rápida utilizando varios modelos de redes neuronales de Keras. Podemos usar hyperas para aprovechar el poder de los hyperopt sin tener que aprender una sintaxis sofisticada.
Definimos un modelo de Keras usando una notación de plantilla simple para definir los hiperparámetros a ajustar para obtener un modelo de red neuronal sintonizado. Es posible que nuestras máquinas tradicionales no puedan proporcionar la potencia informática necesaria para escribir aplicaciones que requieran hardware sofisticado y potencia de procesamiento. Google Colab, puede incluso fallar cuando queremos trabajar con mecanismos sofisticados de aprendizaje de redes neuronales.
En tales casos, optamos por un servicio en la nube. Un ejemplo destacado es AWS SageMaker. Podemos utilizar este servicio para definir, construir, entrenar y probar modelos de redes neuronales. Para comenzar a trabajar con SageMaker, primero debemos iniciar sesión en la consola de administración de AWS desde la URL aws.amazon.com. Hacemos clic en la pestaña Iniciar sesión en la consola que se encuentra en la parte superior derecha de la página. Si no hemos iniciado sesión antes, se nos pedirá que proporcionemos nuestras credenciales de AWS.
Podemos usar el campo de búsqueda ubicado justo debajo de Buscar servicios, comenzamos a escribir la palabra SageMaker, y seleccionamos el servicio Amazon SageMaker. Queremos escribir una aplicación Python simple para utilizar las capacidades de hyperas para seleccionar y ajustar hiperparámetros mientras se construye una red neuronal.
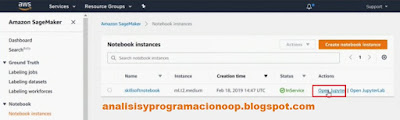
Seleccionamos la opción Instancia de Notebook, del menú izquierdo.
En la página de instancias de Notebook, se nos proporciona cierta información sobre la instancia de Notebook. Como el tipo de instancia, cuándo se creó y el estado actual. Podemos crear una nueva instancia, haciendo clic en el botón Create Notebook Instance. Utilizaremos la instancia existente, por lo que hacemos clic en Abrir Jupyter en la pestaña Acciones.
Seleccionamos el entorno Tensorflow que utilizaremos con Keras y en el cuaderno de jupyter escribimos:
! Pip install hyperas
! Pip install hyperopt
Estas dos declaraciones instalarán hyperas e hyperopt usando el comando pip convencional de Python. Ejecutamos esta celda de código, haciendo clic en el botón de reproducción de radio ubicado justo al lado de la celda de código.
En la siguiente celda de código, importamos las bibliotecas y paquetes necesarios para construir un modelo de red neuronal y trabajar con hiperparámetros.
Estamos importando keras.models, keras.layers, keras.datasets y keras.utils. Este conjunto de importaciones proporcionará los datos junto con las capacidades esenciales de construir modelos de redes neuronales utilizando varios tipos de capas y funciones de activación.
from __future__ import print_function
from hyperopt import trials, STATUS_OK, tpe
from hyperas import optim
from hyperas.distributions import choice, uniform
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.datasets import mnist
from keras.utils import np_utils
A veces, podemos obtener un error si TensorFlow no está instalado y configurado correctamente. La siguiente tarea es definir una función para preparar el modelo de datos. Esta función está separada del modelo de red para garantizar que no necesitemos volver a cargar los datos cada vez que queramos evaluar o volver a ejecutar el modelo.
Estamos construyendo conjuntos de datos X_train, Y_train, X_test e Y_test. Estos son los conjuntos de datos de entrenamiento y prueba. Cargamos los datos usando la declaración, mnist.load_data. Es una función de mnist y mnist es un modelo de datos que importamos de Keras en la celda de código anterior.
def data():
(X_train, y_train), (x_test, y_test) = mnist.load_data ()
A continuación, rellenamos los conjuntos de datos X_train y X_test con los datos de mnist.
X_train = X_train.reshape (60000, 784)
X_test = X_test.reshape (10000, 784)
Hemos tomado 60000 y 784 como dimensiones para X_train. Y hemos hecho lo mismo para X_test, donde la dimensión es 10000 y 784. Después vinculamos X_train y X_test con un tipo de datos particular usando la declaración astype float32. usamos la función astype y pasamos el tipo de datos como float32.
X_train = X_train.astype ('float32')
X_test =
X_test.astype ('float32')
Después factorizamos los datos en los conjuntos de datos de prueba y X_train. dividimos los datos de X_train y los conjuntos de datos de prueba entre 255. Y especificamos el número de clases para la clasificación.
X_train /= 255
X_test /= 255
Suponemos que el número de clases es 10 convertimos Y_train y los conjuntos de datos de prueba en una matriz de clases categórica o binaria pasando los respectivos conjuntos de datos en el número de clases.
Finalmente, devolvemos X_train, Y_train, X_test y Y_test.
nb_classes = 10
Y_train =
np_utils.to_categorical (y_train, nb_classes)
Y_test =
np_utils.to_categorical (y_test, nb_classes)
return X_train, Y_train, X_test, Y_test
En conjunto la celda quedará
def data():
(X_train, y_train), (x_test, y_test) = mnist.load_data ()
X_train = X_train.reshape (60000, 784)
X_test =
X_test.reshape (10000, 784)
X_train =
X_train.astype ('float32')
X_test =
X_test.astype ('float32')
X_train /= 255
X_test /= 255
nb_classes = 10
Y_train =
np_utils.to_categorical (y_train, nb_classes)
Y_test =
np_utils.to_categorical (y_test, nb_classes)
return X_train, Y_train, X_test, Y_test
Hemos creado un modelo de datos que podemos usar para construir y entrenar el modelo de red neuronal. El siguiente paso es construir un modelo de red neuronal. El tipo de modelo que estamos construyendo es un modelo secuencial.
def model (X_train, Y_train, X_test, Y_test):
Agregando una capa densa, que es una operación lineal, donde cada entrada se conectará a cada salida con ciertos pesos, y estamos pasando la forma y las dimensiones de la entrada.
model = Sequential()
Esta será la capa de entrada, y para esta capa estamos usando la función de activación relu.
model.add (Dense (512, input_shape = (784,)))
model.add (Activation ('relu'))
A continuación, agregaremos una capa de salida para garantizar que algunos de los elementos se puedan reducir. Después de agregar la capa de entrada, estamos agregando una capa oculta usando la operación lineal densa a la que estamos pasando la opción.
model.add (Dropout({{uniform (0, 1)}}))
model.add (Dense({{choice([256, 512, 1024])}}))
model.add (Activation({{choice(['relu','sigmoid'])}}))
Hemos agregado múltiples capas para construir nuestra red neuronal.
model.add (Dropout({{uniform (0, 1)}}))
Después de agregar las capas de entrada y ocultas, especificamos una declaración if. Si nuestra elección es cuatro, la declaración agregará otra capa, pero si nuestra elección es tres, usaremos las capas existentes que hemos agregado. También hemos especificado las declaraciones para agregar la cuarta capa, y finalmente estamos agregando la capa de salida utilizando la declaración model.add dense.
if {{choice(['three', 'four'])}} == 'four':
model.add (Dense (100))
model.add ({{choice ([Dropout (0.5), Activation ('linear')])}})
model.add (Activación ('relu'))
model.add (Dense (10))
Y estamos usando la función de activación softmax para la capa de salida.
model.add (Activación ('softmax'))
Así que hemos definido nuestro modelo de red neuronal que contiene múltiples capas, incluida una capa de entrada y una de salida. La celda completa queda:
def model (X_train, Y_train, X_test, Y_test):
model =
Sequential()
model.add (Dense (512, input_shape = (784,)))
model.add (Activation ('relu'))
model.add (Dropout({{uniform (0, 1)}}))
model.add (Dense({{choice([256, 512, 1024])}}))
model.add (Activation({{choice(['relu','sigmoid'])}}))
model.add (Dropout({{uniform (0, 1)}}))
if {{choice(['three', 'four'])}} == 'four':
model.add (Dense (100))
model.add ({{choice ([Dropout (0.5), Activation ('linear')])}})
model.add (Activación ('relu'))
model.add (Dense (10))
model.add (Activación ('softmax'))
La capa de entrada usa relu como función de activación, la capa de salida usa softmax como función de activación, y las capas ocultas o intermedias usan diferentes funciones de activación. Después de definir las capas para el modelo de red neuronal, la siguiente tarea es compilarlo.
Para compilar el modelo, estamos usando la función del modelo llamada compilar, a la que le estamos pasando la entropía cruzada categórica como función de pérdida, ya que hemos convertido el conjunto de datos en categórico.
model.compile(loss = 'categorical_crossentropy',
optimizer = {{choice (['rmsprop', 'adam', 'sgd'])}},
metrics = ['accuracy'])
El segundo argumento es el optimizador. Se utiliza para indicar cómo se debe compilar el modelo o crear una instancia de un objeto. Se especifican tres opciones de optimizador diferentes, rmsprop, adam y sgd, que es la abreviatura de descenso de gradiente estocástico.
El tercer y último argumento que hemos pasado es métrica que le ponemos precisión. Después de compilar el modelo, la siguiente tarea es ajustar el modelo con los conjuntos de datos de entrenamiento.
Estamos usando la función ajustada a la que estamos pasando los conjuntos de datos X e Y_train. Estamos pasando el tamaño del lote, la elección del tamaño del lote es 64 y 128.
model.fit (X_train, Y_train ,
batch_size = {{choice ([64, 128])}},
nb_epoch = 1,
verbose = 2,
validation_data = (X_test, Y_test))
Estamos pasando el número de épocas para la propagación hacia adelante y hacia atrás, y estamos configurando el detallado (verbose) en 2. También estamos pasando otro argumento importante en forma de datos de validación, que se utilizarán para validar el modelo de red neuronal. Los datos de validación que hemos especificado son los conjuntos de datos X e Y_test.
Después de validar el modelo, evaluaremos el modelo y el resultado de la evaluación que estamos usando es la puntuación y la precisión. Estamos usando la función evaluar a la que le estamos pasando los conjuntos de datos X e Y_test seguidos por el detallado que se establece en 0.
score, acc = model.evaluate (X_test, Y_test, verbose = 0)
Hemos establecido verbose en 0 ya que no queremos ningún resultado adicional. Finalmente, imprimimos la precisión de la prueba y devolvemos el factor de pérdida, el estado y el modelo.
print ('Exactitud de la
prueba:', acc)
return {'loss': -acc, 'status': STATUS_OK, 'model': model}
Tenemos que asegurarnos de que estamos especificando valores adecuados. Por ejemplo, hemos especificado menos precisión –acc para el factor de pérdida, STATUS_OK para el modelo de estado, y model para el nombre de nuestro modelo de red neuronal.
Hemos definido nuestra red neuronal, hemos compilado el modelo y hemos aplicado los conjuntos de entrenamiento junto con los datos de validación para asegurar que el modelo esté validado y probado.
Para ejecutar el modelo, hyperas proporciona la función optim.minimize.
appropiate_run, appropiate_model
= optim.minimize (model = model,
data = data,
max_evals = 10,
algo = tpe.suggest,
notebook_name = 'nombre_notebook_de_jupyter', #ojo, esto es importante
trial = Trials ())
Tenemos que pasar el modelo, los datos, el número máximo de evaluaciones que queremos realizar, y el algoritmo que queremos utilizar, que en este caso se sugiere. También tenemos que pasar el nombre del cuaderno, que es el mismo que el del archivo. Y finalmente, también tenemos que aprobar los ensayos, lo que indica el número de ensayos que se realizarán para el modelo actual, con el fin de proporcionar un modelo adecuado y un resultado de ejecución adecuado.
Tras la ejecución, se nos proporcionan ciertos mensajes de registro de salida. Navegaremos más hacia abajo para explorar los resultados del modelo. Podemos observar que el modelo se entrenó con 60.000 muestras y ha utilizado otras 10.000 muestras para su validación. Se ejecutó una sola iteración y se nos proporciona el tiempo que tomó completar la ejecución, seguido del factor de pérdida, precisión, pérdida de validación y precisión de validación.
El resultado final que obtenemos es la precisión de la prueba. Obtendremos 10 resultados de precisión de prueba diferentes, ya que hemos especificado 10 evaluaciones en la celda de código.
Tenemos que esperar a que se completen las validaciones antes de poder observar el resultado final. Se nos proporciona la precisión de la prueba final, que es de 0,96. Se ejecutaron diez de cada diez épocas de validación.
La salida también incluye el mejor factor de pérdida y el tiempo que tomó completar la validación.
El resultado final es el resultado de la selección de hiperparámetros y el ajuste que facilitamos usando hyperas cuando estábamos ejecutando el modelo de red neuronal. Podemos seleccionar diferentes hiperparámetros o ajustar las selecciones de hiperparámetros existentes. Por ejemplo, podemos cambiar las evaluaciones máximas, podemos cambiar el número de épocas, incluso podemos cambiar el tamaño del lote y ejecutar el modelo. Podemos continuar este proceso hasta q